Page 56 - PRE-U STPM MATHEMATICS (T) TERM 1

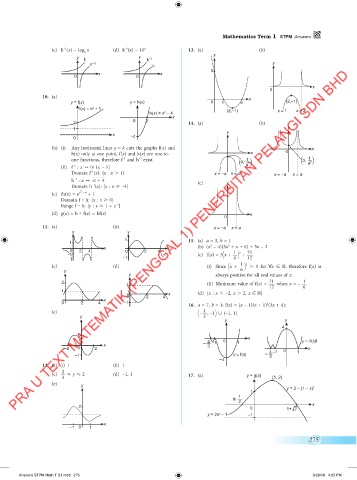
Mathematics Term 1 STPM Answers

–1
(c) h (x) = log x (d) k (x) = 10 x 13. (a) (b)
–1
2
y
y y
h k –1
h –1 k y
3
x x
0 0
x
0
10. (a) x
y = f(x) y = h(x) 0 1 3 (2,–1)
f(x) = e + 1 (2,–1) x = 1 x = 3
x
h(x) = x – 4
2
x
2 0 2 14. (a) (b)
1 y
x y
0 –4
(b) (i) Any horizontal lines y = k cuts the graphs f(x) and x
h(x) only at one point, f(x) and h(x) are one-to- x 0
one functions, therefore f and h exist. 0, 0,
–1
–1
1
1
–
a
( ) – 2 ( ) – 2
a
(ii) f : x ↦ ln (x – 1)
–1
–1
Domain f (x): {x : x . 1} x = –a x = a x = –a x = a
h : x ↦ x + 4
–1
–1
Domain h (x): {x : x > –4} (c) y
2
(c) fh(x) = e x – 4 + 1
Domain f h: {x : x > 0}
°
Range f h: {y : y > 1 + e }
–4
°
(d) g(x) = h f(x) = hf(x) x
°
0
11. (a) (b) x = –a x = a
y y
1 15. (a) a = 3, b = 1
1 2 2
x x (b) (x – 4)(3x + x + 6) + 5x – 2
0 2 4 0 2 4 1 2 71
–1 (c) f(x) = 31 x + 2 +
–1 6 12
1
2

(c) (d) (i) Since 1 x + 2 . 0 for ∀x ∈ R, therefore f(x) is
y 6
y always positive for all real values of x.
1
2 (ii) Minimum value of f(x) = 71 when x = –
1 12 6
1
x (d) {x : x , –2, x . 2, x ∈ R}
0 2 4
x –1
2
0 2 4 16. a = 7, b = 1; f(x) = (x – 1)(x + 1) (3x + 4);
4
(e) 1 – , –12 < (–1, 1)
y 3
y y
4
1
x
4 –1 0 1 y = |f(x)|
x – –
3
–2 0 2 x
4 –1 0 1
–1 y = f(x) – –
3
–4
12. (a) (i) 1 (ii) 1
(c) 2 < y < 2 (d) –1, 1 17. (a) y = g(x)
3 (1, 2)
(e)
y y = 2 – (1 – x) 2
1
1 __
In
2
2 0 1+ 2 x
y = 2e – 1 –1
x
x
– 1 0 1
275
Answers STPM Math T S1.indd 275 3/28/18 4:25 PM