Page 27 - Ranger SPM 2022 - Additional Mathematics

Additional Mathematics SPM Chapter 2 Differentiation

2.1 Limit and Its Relation to Differentiation

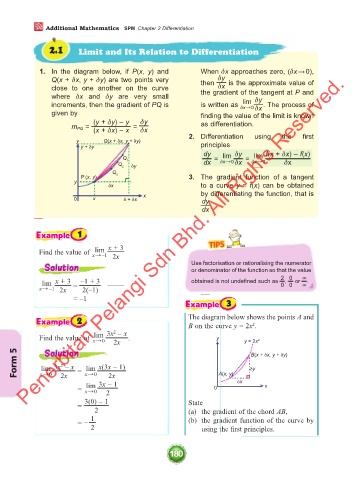
1. In the diagram below, if P(x, y) and When δx approaches zero, (δx → 0),
Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
Q(x + δx, y + δy) are two points very then δy is the approximate value of
δx
close to one another on the curve the gradient of the tangent at P and
where δx and δy are very small δy
lim
increments, then the gradient of PQ is is written as δx : 0 δx . The process of
given by finding the value of the limit is known
(y + δy) – y δy as differentiation.
m PQ = (x + δx) – x = δx
2. Differentiation using the first
y Q(x + δx, y + δy) principles
y + δy
dy lim δy lim f(x + δx) – f(x)
Q 1 = δx : 0 δx =
Q 2 δy dx δx : 0 δx
Q
P (x, y) 3 3. The gradient function of a tangent
y
δx to a curve y = f(x) can be obtained
0 x x + δx x by differentiating the function, that is
dy
dx .

Example 1

lim
Find the value of x : –1 x + 3 TIPS
2x
Use factorisation or rationalising the numerator
Solution or denominator of the function so that the value
2 0
∞
lim x + 3 = –1 + 3 obtained is not undefined such as , or .
0 0
∞
x : –1 2x 2(–1)
= –1
Example 3
Example 2 The diagram below shows the points A and
2
B on the curve y = 2x .
2
lim
Find the value of x : 0 3x – x . y y = 2x 2
2x
Form 5 x : 0 3x – x = x : 0 x(3x – 1) A(x, y) δy
B(x + δx, y + δy)
Solution
2
lim
lim
2x
2x
lim
= x : 0 3x – 1 0 δx x
2
3(0) – 1 State
=
2 (a) the gradient of the chord AB,
1 (b) the gradient function of the curve by
= –
2 using the first principles.
180

02 Ranger Mate Tambahan Tg5.indd 180 25/02/2022 9:23 AM