Page 41 - TI Journal 18-1

DIFFUSION IMAGING FIBER BUNDLES 35

characteristics of a single fiber (e.g., the length, the (Figure 2a right) or automatically selected with clus-
average curvature, the average fractional anisotropy, tering algorithms (Figure 2b). Geometric hulls (7)
etc.). Metrics can also be applied to fiber bundles can be wrapped around the boundary of the fiber
which contain a group of fibers—e.g., the number of bundles to better illustrate the shape and size of the
fibers, the total length of all fibers, the total summed fiber bundles (Figure 2c). Alternative methods have
length of all fibers in the bundle after weighting each been proposed, such as projecting the 3D curves to
fiber by its average fractional anisotropy, etc. (9). The 2D points while preserving the similarities among
fiber bundle metrics are likely influenced by brain the fibers (Figure 2d) (6).
size and, thus, may require further correction. The
metrics can be normalized by the size of the brain, HARDI FIBER BUNDLES
or the intracranial volume, which may provide a bet- As a model for diffusion imaging, diffusion tensor
ter index of brain size prior to the impact of age and has limitations. More than one fiber orientation (e.g.,
pathology. in crossing or kissing fibers) may exist within a single
imaging voxel, and simple diffusion tensor meth-
VISUALIZATION ods are limited in the recovery of structures in areas
Complementary to the quantitative metrics of with complex intra-voxel heterogeneity. To address
diffusion fiber bundles, visualization provides an intu- this problem, high angular resolution diffusion imag-
itive and direct means to explore these fiber bundles. ing (HARDI) techniques were developed to resolve
Diffusion fibers form complicated shapes in brain local crossing fibers within a voxel. Using HARDI,
white matter echoing the shapes of the neural fiber the orientation distribution functions (ODF) for
bundles. The challenge in visualization includes the describing the diffusion profile allow multiple max-
amount of fibers, the complexity of the fiber shapes, ima and, thus, capture complex fiber structures, such
and the multivariate nature of the tensor data. The as crossing, kissing, merging, curving, and fanning
3D diffusion fibers generated from the tractography fibers.
can be visualized with 3D curves, or streamtubes HARDI-based tractography algorithms can be
(23), that use cross section shape and color to map classified as deterministic or probabilistic. Deter-
additional tensor properties like the eigenvectors ministic tracking methods such as streamlines (3)
and anisotropy (Figure 2a left). Fiber bundles can or variations of streamlines (15) in 3D are often
be manually selected by setting regions-of-interests used because of their efficient computation.

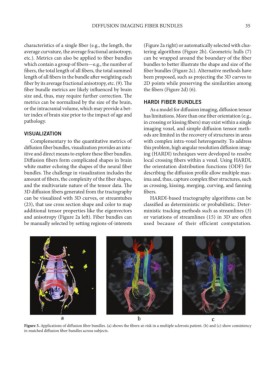
Figure 3. Applications of diffusion fiber bundles. (a) shows the fibers-at-risk in a multiple sclerosis patient. (b) and (c) show consistency
in matched diffusion fiber bundles across subjects.