Page 50 - Engineering Mathematics Workbook_Final

Calculus

2
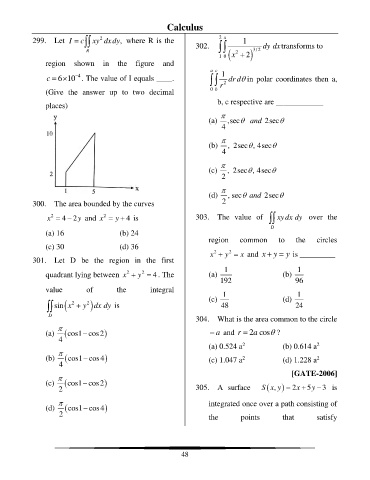
299. Let I = c  xy dxdy , where R is the 2 x 1
R 302.   2 3/ 2 dy dxtransforms to
1 0 ( x + ) 2
region shown in the figure and
a c
−
4
c = 6 10 . The value of I equals ____.  1 2  dr d in polar coordinates then a,

(Give the answer up to two decimal 0 b r
b, c respective are ____________
places)


(a) ,sec  and 2sec
4


(b) , 2sec , 4sec
4


(c) , 2sec , 4sec
2

(d)  , sec and 2sec

300. The area bounded by the curves 2

−
x = 2 4 2y and x = 2 y + 4 is 303. The value of  xydx dy over the
D
(a) 16 (b) 24
region common to the circles
(c) 30 (d) 36
+
x + 2 y = 2 x and x y = y is _________
301. Let D be the region in the first
1 1
quadrant lying between x + 2 y = 2 4 . The (a) (b)
192 96
value of the integral 1 1
(c) (d)
 sin ( x + y 2 ) dx dy is 48 24
2
D
304. What is the area common to the circle

(a) (cos1 cos2− ) = a and r = 2a cos ?
4
2
2
(a) 0.524 a (b) 0.614 a

)
−
(b) (cos1 cos4 (c) 1.047 a (d) 1.228 a 2
2
4
[GATE-2006]

(c) (cos1 cos2− ) 305. A surface ( , x y = 2x +
)
3
2 S 5y − is
 integrated once over a path consisting of
(d) (cos1 cos4− )
2 the points that satisfy

48