Page 647 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

21.1 LA REGLA DEL TRAPECIO 623

o

I (b – a) × altura promedio (21.5)
donde, para la regla del trapecio, la altura promedio es el promedio de los valores de la
función en los puntos extremos, o [f(a) + f(b)]/2.
Todas las fórmulas cerradas de Newton-Cotes se expresan en la forma general de la
ecuación (21.5). De hecho, sólo difieren respecto a la formulación de la altura promedio.

21.1.1 Error de la regla del trapecio

Cuando empleamos la integral bajo un segmento de línea recta para aproximar la integral
bajo una curva, obviamente se tiene un error que puede ser importante (figura 21.6). Una
estimación al error de truncamiento local para una sola aplicación de la regla del trape-
cio es (cuadro 21.2)

E =− 1 f ′′()(ξ b a− ) 3 (21.6)
t
12

donde ξ está en algún lugar en el intervalo de a a b. La ecuación (21.6) indica que si la
función sujeta a integración es lineal, la regla del trapecio será exacta. De otra manera,
para funciones con derivadas de segundo orden y de orden superior (es decir, con cur-
vatura), puede ocurrir algún error.

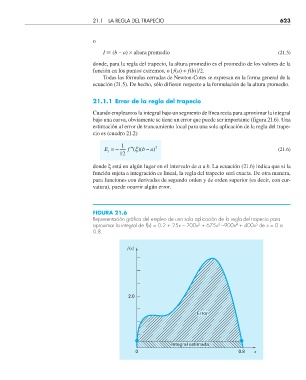
FIGURA 21.6
Representación gráfi ca del empleo de una sola aplicación de la regla del trapecio para
4
3
2
aproximar la integral de f(x) = 0.2 + 25x – 200x + 675x –900x + 400x de x = 0 a
5
0.8.
f(x)

2.0

Error

Integral estimada
0 0.8 x

6/12/06 13:59:42
Chapra-21.indd 623
Chapra-21.indd 623 6/12/06 13:59:42