Page 661 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

21.2 REGLAS DE SIMPSON 637

f (x)

3

2

1
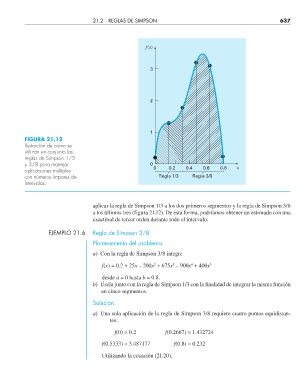
FIGURA 21.12
Ilustración de cómo se
utilizan en conjunto las
reglas de Simpson 1/3
y 3/8 para manejar 0 x
aplicaciones múltiples 0 0.2 0.4 0.6 0.8
con números impares de Regla 1/3 Regla 3/8
intervalos.

aplicar la regla de Simpson 1/3 a los dos primeros segmentos y la regla de Simpson 3/8
a los últimos tres (figura 21.12). De esta forma, podríamos obtener un estimado con una
exactitud de tercer orden durante todo el intervalo.

EJEMPLO 21.6 Regla de Simpson 3/8
Planteamiento del problema.

a) Con la regla de Simpson 3/8 integre
3
2
4
f(x) = 0.2 + 25x – 200x + 675x – 900x + 400x 5
desde a = 0 hasta b = 0.8.
b) Úsela junto con la regla de Simpson 1/3 con la fi nalidad de integrar la misma función
en cinco segmentos.
Solución.

a) Una sola aplicación de la regla de Simpson 3/8 requiere cuatro puntos equidistan-
tes:

f(0) = 0.2 f(0.2667) = 1.432724
f(0.5333) = 3.487177 f(0.8) = 0.232

Utilizando la ecuación (21.20),

6/12/06 13:59:47
Chapra-21.indd 637 6/12/06 13:59:47
Chapra-21.indd 637