Page 730 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

706 EPÍLOGO: PARTE SEIS

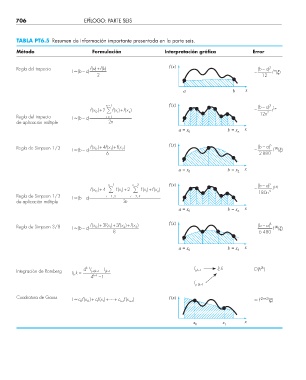
TABLA PT6.5 Resumen de información importante presentada en la parte seis.
Método Formulación Interpretación gráfi ca Error

Regla del trapecio fa()+ f b() f(x) (– ) a 3
b
I (– a) – f ′′ ( )ξ
b
2 12
a b x

n − 1 f(x) (– ) a 3
b
fx( 0 )+2 fx( )+ fx( ) – 2 f ′′
n
i
Regla del trapecio I (– a) i = 1 12n
b
de aplicación múltiple 2 n
a = x 0 b = x n x
Regla de Simpson 1/3 fx( 0 )+ 4 fx( )+ fx( ) f(x) (– )b a 5 ()4 ( )ξ
2
1
I (– a) – f
b
6 2 880
a = x 0 b = x 2 x
n − 1 n − 2 f(x) (– )b a 5 ()4
)+ 4 fx i ()+2 fx i ()+ ( ) – f
fx( 0 fx n 180n 4
Regla de Simpson 1/3 I (– a) i = 1,3 i = 2, 4
b
de aplicación múltiple n 3
a = x 0 b = x n x

Regla de Simpson 3/8 I (– a) fx( 0 )+3 fx( )+3 fx( )+ fx( ) f(x) – (– )b a 5 f ()4 ( )ξ
1
3
2
b
8 6 480
a = x 0 b = x 3 x

4 k–1 I I – l jk,–1 lj k, Oh( 2 k )
Integración de Romberg Ij k, = j ,–11 j k,–1
+
k
4 k–1 –1
l j ,–11+ k
Cuadratura de Gauss I c fx( 0 ) + cfx( ) + + c fx( n 1– ) f(x) f (2 n 2+ ) ()ξ
0
n 1–
1
1
x 0 x 1 x

6/12/06 14:01:22
Chapra-24.indd 706 6/12/06 14:01:22
Chapra-24.indd 706