Page 757 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

25.2 MEJORAS DEL MÉTODO DE EULER 733

y
Pendiente = f(x i +1 , y 0 i +1 )

Pendiente =
f(x , y )
i
i

x i x i +1 x
a)

y f(x , y )+ f(x , y 0 )
Pendiente = i i i +1 i +1
2

x i x i +1 x
b)

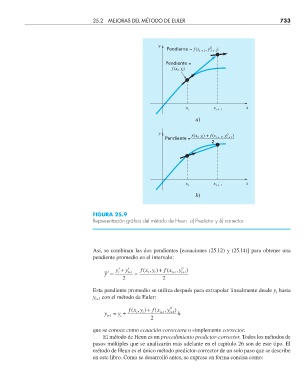
FIGURA 25.9
Representación gráfi ca del método de Heun. a) Predictor y b) corrector.

Así, se combinan las dos pendientes [ecuaciones (25.12) y (25.14)] para obtener una
pendiente promedio en el intervalo:
(,
i
i
y ′ = y i ′ + ′ y + i 1 = f x y ) + f x ( + i 1 y , 0 + i 1 )
2 2
Esta pendiente promedio se utiliza después para extrapolar linealmente desde y i hasta
con el método de Euler:
y i+1
0
(, )
fx y + ( y )
fx ,
y i+1 = y + i i i+1 i+1 h
i
2
que se conoce como ecuación correctora o simplemente corrector.
El método de Heun es un procedimiento predictor-corrector. Todos los métodos de
pasos múltiples que se analizarán más adelante en el capítulo 26 son de este tipo. El
método de Heun es el único método predictor-corrector de un solo paso que se describe
en este libro. Como se desarrolló antes, se expresa en forma concisa como:

6/12/06 14:01:58
Chapra-25.indd 733 6/12/06 14:01:58
Chapra-25.indd 733