Page 96 - analysis-and-interpretation-of-astronomical-sp

Analysis and Interpretation of Astronomical Spectra 96

21 Spectroscopic Determination of Interstellar Extinction

21.1 Spectroscopic Definition of the Interstellar Extinction
With the Balmer-Decrement , the interstellar extinction can spectroscopically be deter-
mined. The extinction parameter characterises the entire extinction along the line of sight
between the object and the outer edge of Earth's atmosphere. It is defined as the logarith-
mic ratio between the theoretical (Th) and measured (obs) intensity of the line [8]:

, also called “logarithmic Balmer-Decrement” [201], is determined by the ratio be-

tween the measured and theoretical Balmer-Decrement and . The value –0.35 cor-

responds to the extinction factor at , according to the standard extinction curve

from Osterbrock (chart below) [201].

In the context of such calculations in the literature the value (Case B) has been

established for the theoretical Balmer-Decrement. inserted in yields:

21.2 Extinction Correction with the Measured Balmer-Decrement

The extinction is not constant but depends on the wavelength. With the correction function
[10], the emission lines are adapted relatively to (“Dereddening”).

is defined as follows, where is the extinction at and .

Thus, the measured intensities are reduced for and raised for (note

the sign of )! The value of is determined with an extinction curve, which exists in

different versions with slightly different values. For amateur applications intermediate val-

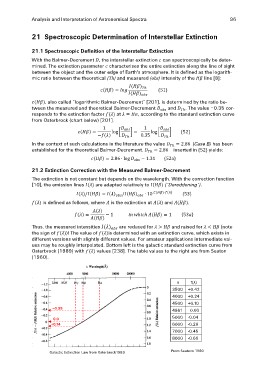
ues may be roughly interpolated. Bottom left is the galactic standard extinction curve from
Osterbrock (1989) with values [238]. The table values to the right are from Seaton

(1960).

–0.35 λ f(λ)
0.0 3500 +0.42
+0.14 4000 +0.24
4500 +0.10
Galactic Extinction Law from Osterbrock1989 4861
5000 0.00
6000 -0.04
7000 -0.26
8000 -0.45
-0.60

From Seatons 1960