Page 221 - Matematik Tingkata 3

Bab 8 Lokus dalam Dua Dimensi

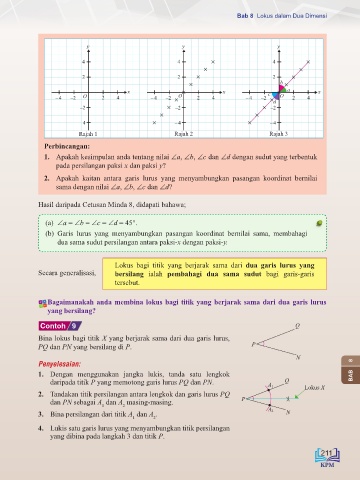
y y y

4 4 × 4 ×
× ×
2 2 × 2 ×
× b ×
x × x c × a x
–4 –2 O 2 4 –4 –2 × O 2 4 –4 –2 × O 2 4

d
–2 × –2 × –2
× ×

–4 × –4 × –4

Rajah 1 Rajah 2 Rajah 3
Perbincangan:
1. Apakah kesimpulan anda tentang nilai ∠a, ∠b, ∠c dan ∠d dengan sudut yang terbentuk
pada persilangan paksi x dan paksi y?
2. Apakah kaitan antara garis lurus yang menyambungkan pasangan koordinat bernilai
sama dengan nilai ∠a, ∠b, ∠c dan ∠d?

Hasil daripada Cetusan Minda 8, didapati bahawa;

(a) ∠a = ∠b = ∠c = ∠d = 45°.
(b) Garis lurus yang menyambungkan pasangan koordinat bernilai sama, membahagi
dua sama sudut persilangan antara paksi-x dengan paksi-y.

Lokus bagi titik yang berjarak sama dari dua garis lurus yang
Secara generalisasi, bersilang ialah pembahagi dua sama sudut bagi garis-garis
tersebut.

Bagaimanakah anda membina lokus bagi titik yang berjarak sama dari dua garis lurus
yang bersilang?

Contoh 9 Q
Bina lokus bagi titik X yang berjarak sama dari dua garis lurus,
PQ dan PN yang bersilang di P. P
N
Penyelesaian: 8
1. Dengan menggunakan jangka lukis, tanda satu lengkok BAB
daripada titik P yang memotong garis lurus PQ dan PN. Q
A 1 Lokus X
2. Tandakan titik persilangan antara lengkok dan garis lurus PQ
dan PN sebagai A dan A masing-masing. P
1
2
3. Bina persilangan dari titik A dan A . A 2 N
1
2
4. Lukis satu garis lurus yang menyambungkan titik persilangan Saiz sebenar
yang dibina pada langkah 3 dan titik P.
211