Page 106 - text book form physics kssm 2020

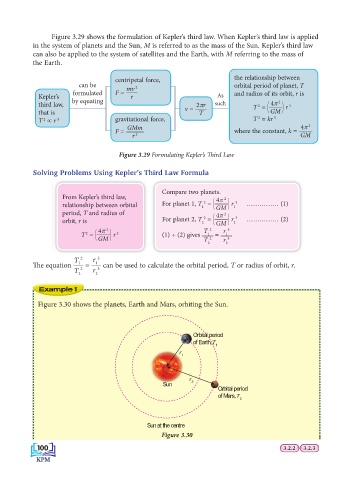
Figure 3.29 shows the formulation of Kepler’s third law. When Kepler’s third law is applied
in the system of planets and the Sun, M is referred to as the mass of the Sun. Kepler’s third law
can also be applied to the system of satellites and the Earth, with M referring to the mass of
the Earth.

centripetal force, the relationship between
can be mv 2 orbital period of planet, T
formulated F = and radius of its orbit, r is
Kepler’s r As
by equating 4π 2
third law, 2πr such 2 3
v = T = r
that is T GM
2
3
2
T ∝ r gravitational force, T = kr 3
GMm 4π 2
F = where the constant, k =
r 2 GM
Figure 3.29 Formulating Kepler’s Th ird Law
Solving Problems Using Kepler’s Third Law Formula

Compare two planets.
From Kepler’s third law, 4π 2
1
r
2
relationship between orbital For planet 1, T = GM 1 3 …………… (1)
period, T and radius of 4π 2
2
2
r
orbit, r is For planet 2, T = GM 2 3 …………… (2)
2
T = 4π 2 r 3 (1) ÷ (2) gives T 1 2 = r 1 3
GM T 2 r 3
2 2
T 2 r 3
Th e equation 1 = 1 can be used to calculate the orbital period, T or radius of orbit, r.
T 2 r 3
2 2
Example 1
Figure 3.30 shows the planets, Earth and Mars, orbiting the Sun.

Orbital period
of Earth,T
1
r
1

r
Sun 2
Orbital period
of Mars,T
2

Sun at the centre

Figure 3.30
100 3.2.2 3.2.3
100
3.2.3
3.2.2