Page 119 - Matematik_Tingkatan_2

Bab 6 Bentuk Geometri Tiga Dimensi Bab 6 Bentuk Geometri Tiga Dimensi

Isi padu prisma
JOM CUBA 6.3
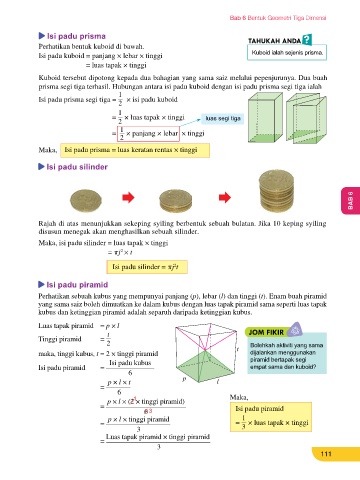
Perhatikan bentuk kuboid di bawah.
1. Hitung luas permukaan objek bentuk geometri tiga dimensi berikut. Isi padu kuboid = panjang × lebar × tinggi Kuboid ialah sejenis prisma.
(a) (b) (c) = luas tapak × tinggi
Kuboid tersebut dipotong kepada dua bahagian yang sama saiz melalui pepenjurunya. Dua buah
12 cm prisma segi tiga terhasil. Hubungan antara isi padu kuboid dengan isi padu prisma segi tiga ialah
14 cm 4 cm 1
Isi padu prisma segi tiga = × isi padu kuboid
2
6 cm 1
5 cm 6 cm 3 cm = × luas tapak × tinggi luas segi tiga
2
1
2. Hitung luas permukaan objek berikut. = × panjang × lebar × tinggi
2
(a) (b) (c)
Maka, Isi padu prisma = luas keratan rentas × tinggi
20 cm Isi padu silinder
260 mm 45 cm

BAB 6 72 mm 30 cm 83 cm BAB 6

3. Hitung luas permukaan gabungan bentuk geometri tiga dimensi berikut.
(a) (b) (c) Rajah di atas menunjukkan sekeping syiling berbentuk sebuah bulatan. Jika 10 keping syiling
Diameter hemisfera
= 10 cm disusun menegak akan menghasilkan sebuah silinder.
j = 5 cm Maka, isi padu silinder = luas tapak × tinggi
2
12 cm 15 cm = πj × t
12 cm
Isi padu silinder = πj t
2
Isi padu piramid
10 cm
Perhatikan sebuah kubus yang mempunyai panjang (p), lebar (l) dan tinggi (t). Enam buah piramid
6.4 Isi Padu Bentuk Tiga Dimensi yang sama saiz boleh dimuatkan ke dalam kubus dengan luas tapak piramid sama seperti luas tapak
kubus dan ketinggian piramid adalah separuh daripada ketinggian kubus.
6.4.1 Menerbitkan rumus Luas tapak piramid = p × l
t
Isi padu prisma dan silinder Menerbitkan rumus isi padu Tinggi piramid = Bolehkah aktiviti yang sama
2
prisma dan silinder, dan maka, tinggi kubus, t = 2 × tinggi piramid t dijalankan menggunakan
Isi padu suatu bentuk geometri tiga dimensi ialah ukuran ruang yang seterusnya membentuk Isi padu kubus piramid bertapak segi
memenuhi bentuk geometri tiga dimensi tersebut. Bentuk ini diukur rumus piramid dan kon. Isi padu piramid = empat sama dan kuboid?
dalam unit padu seperti milimeter padu (mm ), sentimeter padu 6 p
3
(cm ) atau meter padu (m ). Perhatikan bentuk geometri tiga dimensi = p × l × t l
3
3
di bawah. Apakah hubungan antara keratan rentas dengan tapak? 6 Maka,
1
p × l × (2 × tinggi piramid)
= Isi padu piramid
Keratan rentas 6 3
Keratan rentas p × l × tinggi piramid 1
Tapak = = × luas tapak × tinggi
3
3
Tapak Luas tapak piramid × tinggi piramid
=
3
110 111