Page 120 - Matematik_Tingkatan_2

Bab 6 Bentuk Geometri Tiga Dimensi Bab 6 Bentuk Geometri Tiga Dimensi

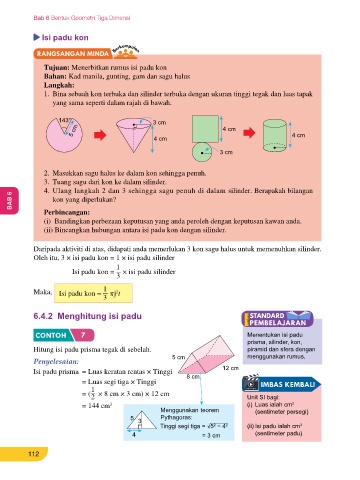
Isi padu kon CONTOH 8
22 Isi padu objek tiga dimensi
Hitung isi padu silinder tegak di sebelah. (Guna π = )
7 berbentuk serong.
Tujuan: Menerbitkan rumus isi padu kon Penyelesaian:
Bahan: Kad manila, gunting, gam dan sagu halus Isi padu silinder = Luas keratan rentas × Tinggi 7 cm t
Langkah: 
2
1. Bina sebuah kon terbuka dan silinder terbuka dengan ukuran tinggi tegak dan luas tapak = πj t j
yang sama seperti dalam rajah di bawah. 22
= ( × 3.5 cm × 3.5 cm) × 12 cm 12 cm
7 t
143° 3 cm = 462 cm 3 
5 cm 4 cm
4 cm 4 cm t = tinggi kon
CONTOH 9 B = luas tapak
3 cm 22 1
Hitung isi padu kon tegak di sebelah. (Guna π = ) I = Bt
7 3
Penyelesaian: 1
2. Masukkan sagu halus ke dalam kon sehingga penuh. 1 I = πj t
2
3
3. Tuang sagu dari kon ke dalam silinder. Isi padu kon = × Luas tapak × Tinggi
3
4. Ulang langkah 2 dan 3 sehingga sagu penuh di dalam silinder. Berapakah bilangan = 1 πj t 12 cm
BAB 6 kon yang diperlukan? 3 t t BAB 6
2
Perbincangan: = 1 × ( 22 × 7 cm × 7 cm) × 12 cm
(i) Bandingkan perbezaan keputusan yang anda peroleh dengan keputusan kawan anda. 3 7 7 cm
1
(ii) Bincangkan hubungan antara isi padu kon dengan silinder. = 616 cm 3 Isi padu = Bt
3
Daripada aktiviti di atas, didapati anda memerlukan 3 kon sagu halus untuk memenuhkan silinder. CONTOH 10
Oleh itu, 3 × isi padu kon = 1 × isi padu silinder Hitung isi padu piramid tegak di sebelah. V
1
Isi padu kon = × isi padu silinder
3 Penyelesaian:
1
1
Maka, Isi padu kon = πj t Isi padu piramid = × Luas tapak × Tinggi 3 cm
2
3
3 B
= 1 × (4 cm × 4 cm) × 3 cm
3
6.4.2 Menghitung isi padu A C
= 16 cm 3
4 cm
CONTOH 7 Menentukan isi padu D
prisma, silinder, kon,
Hitung isi padu prisma tegak di sebelah. piramid dan sfera dengan Isi padu sfera
5 cm menggunakan rumus.
Penyelesaian:
Isi padu prisma = Luas keratan rentas × Tinggi 8 cm 12 cm Sfera ialah satu bentuk geometri tiga dimensi yang mempunyai satu titik tetap yang dikenali sebagai
= Luas segi tiga × Tinggi pusat sfera. Semua titik pada permukaannya mempunyai jarak yang sama dari pusat sfera. Isi padu
sfera yang mempunyai jejari, j ialah
1
= ( × 8 cm × 3 cm) × 12 cm Unit SI bagi:
2
2
= 144 cm 3 (i) Luas ialah cm 4
Menggunakan teorem (sentimeter persegi) Isi padu sfera = πj 3
5 3 Pythagoras: 3 j
Tinggi segi tiga = �5 − 4 (ii) Isi padu ialah cm
3
2
2
4 = 3 cm (sentimeter padu)
112 113