Page 265 - Matematik_Tingkatan_2

Bab 12 Sukatan Kecenderungan Memusat Bab 12 Sukatan Kecenderungan Memusat

Penyelesaian:
(a) RM1, RM2, RM3, RM3, RM6 Tujuan: Mengorganisasikan data mengikut kumpulan atau kelas
RM1 + RM2 + RM3 + RM3 + RM6
Min = 5 Median = RM3 Mod = RM3 Bahan: Lembaran kerja, penimbang
RM15 Langkah:
=
5 1. Setiap murid di dalam kelas dikehendaki menimbang berat masing-masing dan catatkan
= RM3 berat itu pada papan putih. Berat (kg) Gundal Kekerapan
2. Organisasikan data berat, dalam kg, yang didapati itu
(b) (i) Data baharu apabila nilai asal ditambah RM2 ialah RM3, RM4, RM5, RM5 dan RM8. dalam jadual di sebelah mengikut selang kelas berikut. 30 - 39
RM3 + RM4 + RM5 + RM5 + RM8 40 - 49
Min = 5 Median = RM5 Mod = RM5 30 - 39, 40 - 49, 50 - 59, 60 - 69, 70 - 79 50 - 59
RM25 4. Gundal dan lengkapkan jadual kekerapan di sebelah.
= 60 - 69
5 Nilai median asal juga Nilai mod asal juga Perbincangan:
= RM5 Nilai min asal juga ditambah RM2 ditambah RM2 ditambah RM2 Apakah perbezaan antara jadual kekerapan data 70 - 79
terkumpul dengan jadual kekerapan data tak terkumpul yang telah anda pelajari sebelum ini?
(ii) Data baharu apabila nilai asal didarab 3 ialah RM3, RM6, RM9, RM9 dan RM18.
RM3 + RM6 + RM9 + RM9 + RM18 Daripada aktiviti rangsangan minda di atas, kita mendapati bahawa bagi jadual kekerapan data
Min = 5 Median = RM9 Mod = RM9
RM45 terkumpul, data diklasifikasikan dalam kelas tertentu dengan selang yang seragam.
= Nilai median asal Nilai mod asal
5 Kelas ini dapat mengkategorikan data itu kepada beberapa kumpulan yang sesuai seperti gred
= RM9 Nilai min asal juga didarab 3 juga didarab 3 juga didarab 3 keputusan, lulus atau gagal, tahap pencapaian dan sebagainya. Maklumat-maklumat ini akan

Berdasarkan contoh tersebut, apabila data diubah secara seragam, nilai min, median dan mod yang membantu kita membuat rumusan.
baharu juga berubah secara seragam. Situasi ini sangat penting apabila kita ingin mengorganisasikan set data yang besar.

CONTOH 14 CONTOH 15 Markah Matematik

Tingkatan 2 Zuhal
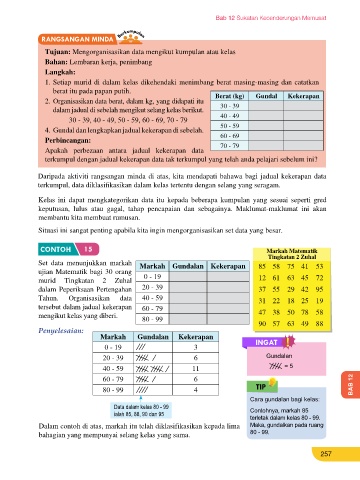
Skor Raju dalam kuiz bahasa Jepun ialah 3, 6 dan 6. Set data menunjukkan markah
(a) Hitung min, median dan mod bagi set data itu. ujian Matematik bagi 30 orang Markah Gundalan Kekerapan 85 58 75 41 53
(b) Tambahkan data pertama dengan 1, tambahkan data kedua dengan 2 dan tambahkan data murid Tingkatan 2 Zuhal 0 - 19 12 61 63 45 72
ketiga dengan 3. Seterusnya, hitung nilai min, median dan mod yang baharu. dalam Peperiksaan Pertengahan 20 - 39 37 55 29 42 95
Tahun. Organisasikan data 40 - 59
Penyelesaian: tersebut dalam jadual kekerapan 60 - 79 31 22 18 25 19

(a) Min = 3 + 6 + 6 , Median = 6, Mod = 6 (b) Data baharu ialah (3 + 1), (6 + 2), (6 + 3) iaitu mengikut kelas yang diberi. 80 - 99 47 38 50 78 58
3
15 4, 8 dan 9. 90 57 63 49 88
= Penyelesaian:
3 4 + 8 + 9 Markah Gundalan Kekerapan
= 5 Min = 3 , Median = 8, Tiada mod 0 - 19 3 INGAT !
Berdasarkan contoh tersebut, apabila data = 21 20 - 39 6 Gundalan
diubah secara tidak seragam, nilai min, 3 40 - 59 11 = 5
median dan mod yang baharu juga berubah = 7 60 - 79 6
BAB 12 12.1.3 Mengorganisasikan data bagi jadual 80 - 99 4 BAB 12
secara tidak seragam.

kekerapan data terkumpul Data dalam kelas 80 - 99 Cara gundalan bagi kelas:
Contohnya, markah 85
Mengumpul data, ialah 85, 88, 90 dan 95 terletak dalam kelas 80 - 99.
Jadual kekerapan bagi data terkumpul membina dan mentafsir Dalam contoh di atas, markah itu telah diklasif ikasikan kepada lima Maka, gundalkan pada ruang
jadual kekerapan bagi 80 - 99.
data terkumpul. bahagian yang mempunyai selang kelas yang sama.

256 257