Page 39 - Matematik_Tingkatan_2

Bab 2 Pemfaktoran dan Pecahan Algebra Bab 2 Pemfaktoran dan Pecahan Algebra

(c) 3y – 147 (d) 5k – 80 FSTB 5 dan 80 CONTOH 9
2
2
ialah 5
2
2
= 3(y – 49) FSTB 3 dan 147 = 5(k – 16) Faktorkan setiap ungkapan berikut.
ialah 3
2
2
2
2
= 3(y – 7 ) = 5(k − 4 ) 2 2
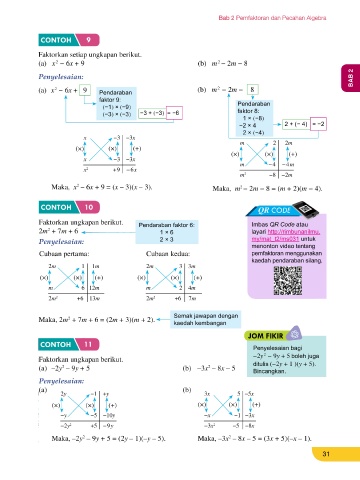
= 3(y+ 7)(y– 7) = 5(k + 4)(k − 4) (a) x − 6x + 9 (b) m − 2m − 8

BAB 2 Penyelesaian: BAB 2
2
2
Suatu ungkapan algebra seperti x + 2xy + y boleh difaktorkan Identiti Pemfaktoran (a) x − 6x + 9 Pendaraban (b) m − 2m − 8
2
2
2
(a) (x + y)
sebagai (x + y)(x + y). = (x + y)(x + y) faktor 9: Pendaraban
2
= x + 2xy + y 2 (−1) × (−9) −3 + (−3) = −6 faktor 8:
(−3) × (−3)
1 × (−8)
Menggunakan pendaraban silang (b) (x – y) 2 −2 × 4 2 + (− 4) = −2
= (x – y)(x – y) x −3 −3x 2 × (−4)
2
Bagi ungkapan algebra berbentuk ax + bx + c dengan a≠0 dan a, = x – 2xy + y 2 (×) (×) (+) m 2 2m
2
b, c ialah suatu integer boleh difaktorkan dengan kaedah pendaraban (c) x – y x −3 −3x (×) (×) (+)
2
2
silang. = (x + y)(x − y) 2 m −4 −4m
x +9 −6x
2
m −8 −2m
Perhatikan contoh di bawah berserta penerangannya untuk pemfaktoran 2
2
ungkapan algebra x + 6x + 8. QR CODE Maka, x – 6x + 9 = (x – 3)(x – 3). Maka, m − 2m − 8 = (m + 2)(m − 4).
2
Langkah 1: Bandingkan pekali Imbas QR Code atau layari CONTOH 10 QR CODE
http://rimbunanilmu.my/
1x + 6x + 8 mat_t2/ms030 di bawah
2
untuk menonton video Faktorkan ungkapan berikut. Pendaraban faktor 6: Imbas QR Code atau
2
tentang kaedah pemfaktoran 2m + 7m + 6 1 × 6 layari http://rimbunanilmu.
a x + b x + c menggunakan jubin algebra. Penyelesaian: 2 × 3 my/mat_t2/ms031 untuk
2
menonton video tentang
Maka, a = 1, b = 6 dan c = 8 Cubaan pertama: Cubaan kedua: pemfaktoran menggunakan
kaedah pendaraban silang.
2m 1 1m 2m 3 3m
Langkah 2: Faktor bagi 8 ialah 1, 2, 4 dan 8. 2 dan 4 dipilih kerana (×) (×) (+) (×) (×) (+)
menepati c , iaitu 2 × 4 = 8.
m 6 12m m 2 4m
Langkah 3: 2 dan 4 dipilih kerana menepati b , iaitu 2 + 4 = 6. 2m +6 13m 2m +6 7m
2
2
Hasil
Langkah 4: Lakukan darab silang seperti di bawah. Tambah Hasil Darab Maka, 2m + 7m + 6 = (2m + 3)(m + 2). Semak jawapan dengan
2
b c kaedah kembangan
x +2 2x 1 + 8 = 9 1 × 8 = 8
−1 + (−8) = −9 −1 × (−8) = 8 CONTOH 11
(×) (×) (+) 2 + 4 = 6 2 × 4 = 8 Penyelesaian bagi
2 + 4 = 6
2 × 4 = 8
2
−2 + (−4) = −6 −2 × (−4) = 8 Faktorkan ungkapan berikut. −2y − 9y + 5 boleh juga
x +4 4x (a) –2y – 9y + 5 (b) –3x – 8x – 5 ditulis (−2y + 1 )(y + 5).
2
2
x +8 6x Bincangkan.
2
Penyelesaian:
Pemfaktoran dan pembahagian (a) (b)
c b x + 4 2y −1 +y 3x 5 −5x
x + 2 x + 6x + 8 (×) (×) (+) (×) (×) (+)
2
Langkah 5: Faktor x + 6x + 8 ialah (x + 2)(x + 4). (−) x + 2x −y −5 −10y −x −1 −3x
2
2
4x + 8
2
(−) 4x + 8 −2y 2 +5 −9y −3x −5 −8x
0 Maka, –2y – 9y + 5 = (2y – 1)(–y – 5). Maka, –3x – 8x – 5 = (3x + 5)(–x – 1).
2
2
30 31