Page 159 - Matematik Tambahan Tingkatan 5 KSSM

Taburan Kebarangkalian

(c) P(X = 0) P(X = 1)
= P(J, J, J) = P(J, J, K) + P(J, K, J) + P(K, J, J)
3 3 3 ( 3 3 5 ) ( 3 5 3 ) ( 5 3 3 )
= × × = × × + × × + × ×
8 8 8 8 8 8 8 8 8 8 8 8
= 27 = 135
512 512
= 0.0527 = 0.2637

P(X = 2)
= P(J, K, K) + P(K, J, K) + P(K, K, J) Kaedah Alternatif
3
5
5
+
= ( 3 × × 5 ) ( 5 × × 5 ) ( 5 × × 3 ) Untuk P(X = 1), peristiwa
+
8
8
memperoleh produk K
8
8
8
8
8
8
8
= 225 boleh berlaku pada cabutan
512 pertama, kedua atau ketiga.
Jadi, konsep gabungan
= 0.4395
boleh digunakan.
P(X = 3) 3 C 1( )( ) ( )( )

5 3 2
5 1 3 2
= 3
8 8
= P(K, K, K) 8 8 135 BAB
5 5 5 = 512
= × × 5
8 8 8 = 0.2637
= 125
512

= 0.2441
KEMENTERIAN PENDIDIKAN MALAYSIA
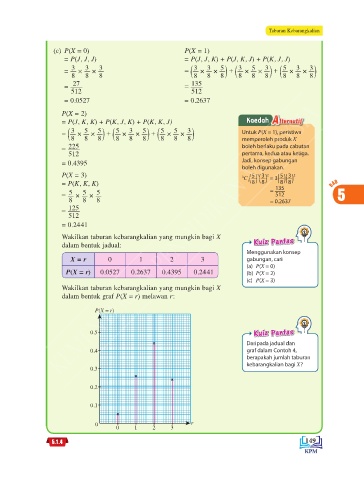
Wakilkan taburan kebarangkalian yang mungkin bagi X
dalam bentuk jadual:
Menggunakan konsep
X = r 0 1 2 3 gabungan, cari
(a) P(X = 0)

P(X = r) 0.0527 0.2637 0.4395 0.2441 (b) P(X = 2)

(c) P(X = 3)
Wakilkan taburan kebarangkalian yang mungkin bagi X
dalam bentuk graf P(X = r) melawan r:
P(X = r)
0.5
Daripada jadual dan
0.4 graf dalam Contoh 4,
berapakah jumlah taburan
kebarangkalian bagi X?

0.3
0.2
0.1
0 r
0 1 2 3
149
5.1.4 149