Page 70 - Matematik Tambahan Tingkatan 5 KSSM

Selain kaedah lakaran tangen bagi suatu fungsi y = f(x), y
2
d y
pembezaan peringkat kedua, jika wujud, boleh P(1, 2)
dx 2
digunakan untuk menentukan sama ada suatu titik pusingan y = 3x – x 3
ialah titik maksimum atau minimum.
x
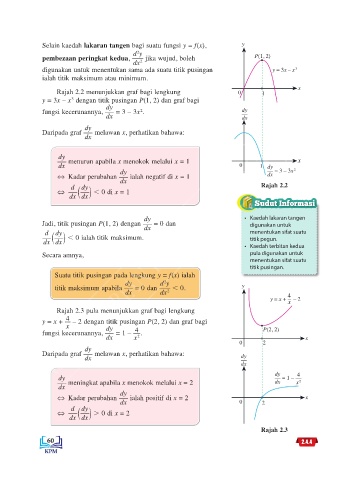
Rajah 2.2 menunjukkan graf bagi lengkung 0 1
3
y = 3x – x dengan titik pusingan P(1, 2) dan graf bagi
KEMENTERIAN PENDIDIKAN MALAYSIA
dy
2
fungsi kecerunannya, = 3 – 3x . dy
––
dx dx
dy
Daripada graf melawan x, perhatikan bahawa:
dx
dy
menurun apabila x menokok melalui x = 1 x
dx 0 1 dy
dy –– = 3 – 3x 2
Í Kadar perubahan ialah negatif di x = 1 dx
dx
d dy Rajah 2.2
Í ( ) , 0 di x = 1
dx dx
Sudut Informasi
Sudut Informasi
dy • Kaedah lakaran tangen
Jadi, titik pusingan P(1, 2) dengan = 0 dan digunakan untuk
dx
d dy menentukan sifat suatu
( ) , 0 ialah titik maksimum. titik pegun.
dx dx
• Kaedah terbitan kedua
Secara amnya, pula digunakan untuk
menentukan sifat suatu
titik pusingan.
Suatu titik pusingan pada lengkung y = f(x) ialah

2
dy d y
titik maksimum apabila = 0 dan , 0. y
dx dx 2 4
–
y = x + – 2
x
Rajah 2.3 pula menunjukkan graf bagi lengkung
4
y = x + – 2 dengan titik pusingan P(2, 2) dan graf bagi
x dy
fungsi kecerunannya, = 1 – 4 . P(2, 2)
dx x 2 x
0 2
dy
Daripada graf melawan x, perhatikan bahawa:
dx dy
––
dx
dy 4
dy –– = 1 – ––
meningkat apabila x menokok melalui x = 2 dx x 2
dx
dy
Í Kadar perubahan ialah positif di x = 2 x
dx 0 2
d dy
Í ( ) . 0 di x = 2
dx dx
Rajah 2.3
60 2.4.4