Page 71 - Matematik Tambahan Tingkatan 5 KSSM

Pembezaan
dy d dy
Jadi, titik pusingan P(2, 2) dengan = 0 dan ( ) . 0 ialah titik minimum.
dx dx dx
Secara amnya,

Suatu titik pusingan pada lengkung y = f(x) ialah titik minimum apabila

dy = 0 dan d y . 0. BAB
2
dx dx 2 2
dy KEMENTERIAN PENDIDIKAN MALAYSIA
Contoh 17

Cari titik-titik pegun bagi setiap lengkung berikut dan tentukan sifat setiap titik pegun itu.
4
2
3
(a) y = 2x + 3x – 12x + 5 (b) y = x – 4x + 1
3
Penyelesaian
3
(a) y = 2x + 3x – 12x + 5
2
dy
= 6x + 6x – 12
2
dx
= 6(x + x – 2)
2
dy
= 6(x + 2)(x – 1)
dx
dy
Untuk titik pegun, = 0
dx
6(x + 2)(x – 1) = 0
x = –2 atau x = 1
2
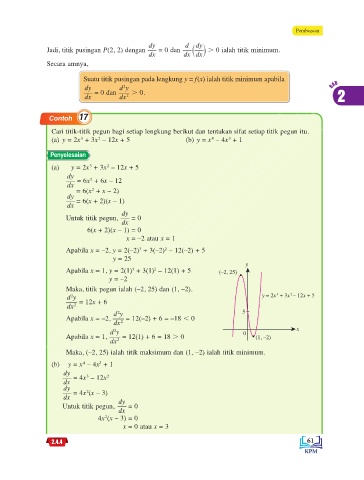
Apabila x = –2, y = 2(–2) + 3(–2) – 12(–2) + 5
3
y = 25
y
3
Apabila x = 1, y = 2(1) + 3(1) – 12(1) + 5 (–2, 25)
2
y = –2
Maka, titik pegun ialah (–2, 25) dan (1, –2).
2
d y y = 2x 3 + 3x 2 – 12x + 5
= 12x + 6
dx 2
2
d y 5
Apabila x = –2, = 12(–2) + 6 = –18 , 0
dx 2
x
2
d y 0
Apabila x = 1, = 12(1) + 6 = 18 . 0 (1, –2)
dx 2
Maka, (–2, 25) ialah titik maksimum dan (1, –2) ialah titik minimum.
3
(b) y = x – 4x + 1
4
= 4x – 12x 2
3
dx
dy
2
= 4x (x – 3)
dx dy
Untuk titik pegun, = 0
dx
4x (x – 3) = 0
2
x = 0 atau x = 3
2.4.4 61