Page 39 - Spotlight A+ SPM Additional Mathematics Form 4 & 5

Form
5 Additional Mathematics Chapter 6 Trigonometric Functions

Concept

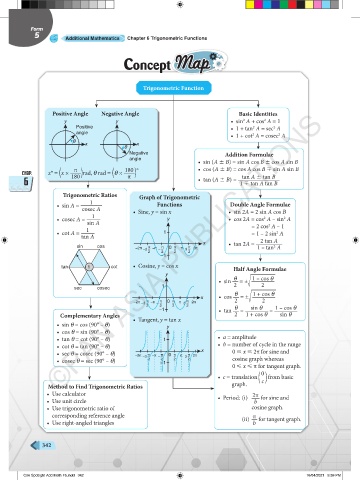
Trigonometric Function

Positive Angle Negative Angle Basic Identities
©PAN ASIA PUBLICATIONS
2
2
y y • sin A + cos A = 1
Positive • 1 + tan A = sec A
2
2
angle
• 1 + cot A = cosec A
2
2
θ
x x
θ
Negative Addition Formulae
angle
• sin (A  B) = sin A cos B  cos A sin B
(
)
(
π
CHAP. x° = x × 180 ) rad, q rad = q × 180 ° • cos (A  B) = cos A cos B  sin A sin B
π
tan A  tan B
6 • tan (A  B) = 1  tan A tan B
Trigonometric Ratios Graph of Trigonometric
1
• sin A = Functions Double Angle Formulae
cosec A • Sine, y = sin x • sin 2A = 2 sin A cos B
1
• cosec A = y • cos 2A = cos A – sin A
2
2
sin A 2
1 = 2 cos A – 1
• cot A = 1 = 1 – 2 sin A
2
tan A
x • tan 2A = 2 tan A
2
sin cos –2π π –π π 0 π π π 2π 1 – tan A
–3 –
2 – – 2 – 2 3 – 2
–1
tan 1 cot • Cosine, y = cos x Half Angle Formulae
y
!
q
• sin = ± 1 – cos q
1 2 2
sec cosec
!
q
x • cos = ± 1 + cos q
–2π –3 – π –π – – π 0 π – π 3 – π 2π 2 2
2 2 2 2 q sin q 1 – cos q
–1 • tan = =
Complementary Angles • Tangent, y = tan x 2 1 + cos q sin q
• sin q = cos (90° – q) y
• cos q = sin (90° – q)
• tan q = cot (90° – q) 1 • a = amplitude
• cot q = tan (90° – q) • b = number of cycle in the range
• sec q = cosec (90° – q) –2π –3 – π –π – – π 0 π – π 3 – π 2π x 0 < x < 2π for sine and
• cosec q = sec (90° – q) 2 –1 2 2 cosine graph whereas
2
0 < x < π for tangent graph.
0
• c = translation ( ) from basic
c
Method to Find Trigonometric Ratios graph.
• Use calculator • Period: (i) 2π for sine and
• Use unit circle b
• Use trigonometric ratio of cosine graph.
corresponding reference angle (ii) π for tangent graph.
• Use right-angled triangles b
342
C06 Spotlight Add Math F5.indd 342 16/04/2021 5:39 PM