Page 41 - Spotlight A+ SPM Additional Mathematics Form 4 & 5

Form
5 Additional Mathematics Chapter 6 Trigonometric Functions

Example 19 Example 20
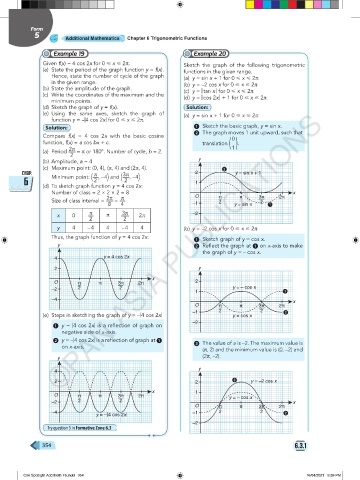
Given f(x) = 4 cos 2x for 0 < x < 2π. Sketch the graph of the following trigonometric
(a) State the period of the graph function y = f(x). functions in the given range.
Hence, state the number of cycle of the graph (a) y = sin x + 1 for 0 < x < 2π
in the given range.
(b) State the amplitude of the graph. (b) y = –2 cos x for 0 < x < 2π
(c) Write the coordinates of the maximum and the (c) y = | tan x | for 0 < x < 2π
minimum points. (d) y = | cos 2x | + 1 for 0 < x < 2π
(d) Sketch the graph of y = f(x). Solution:
(e) Using the same axes, sketch the graph of (a) y = sin x + 1 for 0 < x < 2π
©PAN ASIA PUBLICATIONS
function y = –|4 cos 2x| for 0 < x < 2π.
Solution: 1 Sketch the basic graph, y = sin x.
Compare f(x) = 4 cos 2x with the basic cosine 2 The graph moves 1 unit upward, such that
0
function, f(x) = a cos bx + c. translation ( ) .
(a) Period 2π = π or 180°. Number of cycle, b = 2. 1
2
(b) Amplitude, a = 4 y
(c) Maximum point: (0, 4), (π, 4) and (2π, 4).
CHAP. Minimum point: ( π , –4 and ( 3π , –4 ) 2 y = sin x + 1
)

6 2 2 1
(d) To sketch graph function y = 4 cos 2x:
Number of class = 2 × 2 × 2 = 8 x
Size of class interval = 2π = π O π – 2 π 3π 2π
––
2
8 4 –1 y = sin x

x 0 π π 3π 2π –2
2 2
y 4 – 4 4 – 4 4 (b) y = –2 cos x for 0 < x < 2π
Thus, the graph function of y = 4 cos 2x: 1 Sketch graph of y = cos x.
y 2 Reflect the graph at 1 on x-axis to make
the graph of y = – cos x.
4 y = 4 cos 2x
2 y
x
O π π 3π 2π 2
– ––
–2 2 2 y = – cos x
1
–4 x
O π π 3π 2π
– 2 ––
2
(e) Steps in sketching the graph of y = –|4 cos 2x| –1 y = cos x
1 y = |4 cos 2x| is a reflection of graph on –2
negative side of x-axis.
2 y = –|4 cos 2x| is a reflection of graph at 1 3 The value of a is –2. The maximum value is
on x-axis.
(π, 2) and the minimum value is (0, –2) and
y (2π, –2).
y
4

2 2 y = –2 cos x
x 1
O π π 3π 2π
– –– y = – cos x
–2 2 2 x
O π π 3π 2π
– ––
–4 –1 2 2
y = –|4 cos 2x|
–2
Try question 3 in Formative Zone 6.3
354 6.3.1

C06 Spotlight Add Math F5.indd 354 16/04/2021 5:39 PM