Page 40 - Spotlight A+ SPM Additional Mathematics Form 4 & 5

Form
5
Chapter 6 Trigonometric Functions Additional Mathematics
A Using calculator The following is the trigonometric ratios by using
For the value of cosecant, secant and cotangent, the x-coordinate and y-coordinate in unit circle
value can be calculated by using the reciprocal of the sin q = coordinate-y
following ratios. cos q = coordinate-x
y-coordinate
cosec q = 1 , sec q = 1 , cot q = 1 tan q = x-coordinate
sin q cos q sin q

Example 8 Example 10
©PAN ASIA PUBLICATIONS
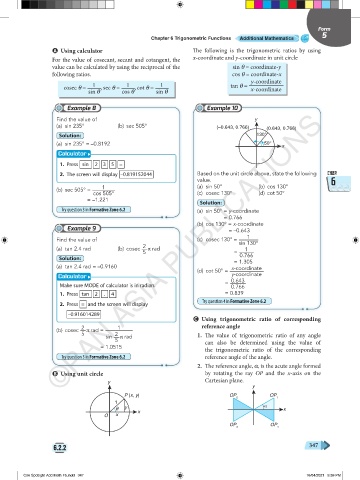
Find the value of y
(a) sin 235° (b) sec 505° (–0.643, 0.766) (0.643, 0.766)
Solution: 130°
(a) sin 235° = –0.8192 50°
x
Calculator
1. Press sin 2 3 5 =
2. The screen will display –0.819152044 Based on the unit circle above, state the following CHAP.
value. 6
(b) sec 505° = 1 (a) sin 50° (b) cos 130°
cos 505° (c) cosec 130° (d) cot 50°
= –1.221
Solution:
Try question 3 in Formative Zone 6.2 (a) sin 50° = y-coordinate
= 0.766
(b) cos 130° = x-coordinate
Example 9 = –0.643
1
Find the value of (c) cosec 130° = sin 130°
(a) tan 2.4 rad (b) cosec 2 π rad 1
5 =
Solution: 0.766
= 1.305
(a) tan 2.4 rad = –0.9160 x-coordinate
(d) cot 50° =
y-coordinate
Calculator 0.643
Make sure MODE of calculator is in radian. = 0.766
1. Press tan 2 . 4 = 0.839
Try question 4 in Formative Zone 6.2
2. Press = and the screen will display
–0.916014289
C Using trigonometric ratio of corresponding

(b) cosec 2 π rad = 1 reference angle
5 sin 2 π rad 1. The value of trigonometric ratio of any angle
5 can also be determined using the value of
= 1.0515
the trigonometric ratio of the corresponding
Try question 3 in Formative Zone 6.2 reference angle of the angle.
2. The reference angle, a, is the acute angle formed
B Using unit circle by rotating the ray OP and the x-axis on the
Cartesian plane.
y
y
P (x, y) OP OP
2 1
1
θ y α x
x
O x
OP OP
3 4

6.2.2 347

C06 Spotlight Add Math F5.indd 347 16/04/2021 5:39 PM