Page 374 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

expresses as a linear combination of the vectors in S with coefficients that are not all zero.

EXAMPLE 8 Using Theorem 5.3.2b

The functions and form a linearly independent set of vectors in , since neither function is a

constant multiple of the other.

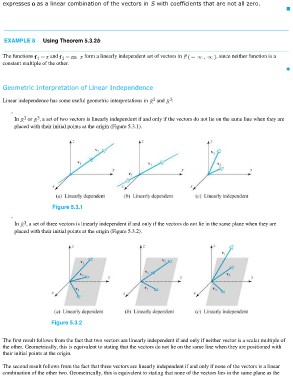
Geometric Interpretation of Linear Independence

Linear independence has some useful geometric interpretations in and :

In or , a set of two vectors is linearly independent if and only if the vectors do not lie on the same line when they are
placed with their initial points at the origin (Figure 5.3.1).

Figure 5.3.1

In , a set of three vectors is linearly independent if and only if the vectors do not lie in the same plane when they are
placed with their initial points at the origin (Figure 5.3.2).

Figure 5.3.2

The first result follows from the fact that two vectors are linearly independent if and only if neither vector is a scalar multiple of
the other. Geometrically, this is equivalent to stating that the vectors do not lie on the same line when they are positioned with
their initial points at the origin.

The second result follows from the fact that three vectors are linearly independent if and only if none of the vectors is a linear
combination of the other two. Geometrically, this is equivalent to stating that none of the vectors lies in the same plane as the