Page 375 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

other two, or, alternatively, that the three vectors do not lie in a common plane when they are positioned with their initial points
at the origin (why?).
The next theorem shows that a linearly independent set in can contain at most n vectors.
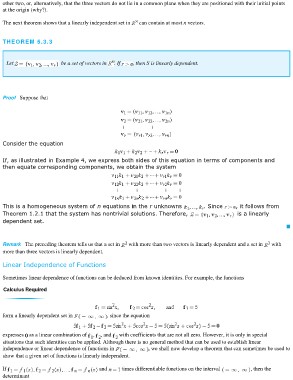
THEOREM 5.3.3

Let be a set of vectors in . If , then S is linearly dependent.

Proof Suppose that

Consider the equation

If, as illustrated in Example 4, we express both sides of this equation in terms of components and
then equate corresponding components, we obtain the system

This is a homogeneous system of n equations in the r unknowns . Since , it follows from
Theorem 1.2.1 that the system has nontrivial solutions. Therefore, is a linearly
dependent set.

Remark The preceding theorem tells us that a set in with more than two vectors is linearly dependent and a set in with
more than three vectors is linearly dependent.

Linear Independence of Functions

Sometimes linear dependence of functions can be deduced from known identities. For example, the functions

Calculus Required

form a linearly dependent set in , since the equation

expresses as a linear combination of , , and with coefficients that are not all zero. However, it is only in special

situations that such identities can be applied. Although there is no general method that can be used to establish linear

independence or linear dependence of functions in , we shall now develop a theorem that can sometimes be used to

show that a given set of functions is linearly independent.

If and times differentiable functions on the interval , then the
determinant