Page 888 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition
P. 888
From 19 and 20, we have
Solving for the , , , and in 14, we obtain the following expression for the interpolating parabolic runout spline:
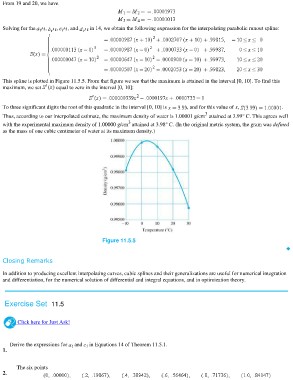
This spline is plotted in Figure 11.5.5. From that figure we see that the maximum is attained in the interval [0, 10]. To find this
maximum, we set equal to zero in the interval [0, 10]:
To three significant digits the root of this quadratic in the interval [0, 10] is , and for this value of x, .
Thus, according to our interpolated estimate, the maximum density of water is 1.00001 g/cm3 attained at 3.99° C. This agrees well
with the experimental maximum density of 1.00000 g/cm3 attained at 3.98° C. (In the original metric system, the gram was defined
as the mass of one cubic centimeter of water at its maximum density.)
Figure 11.5.5
Closing Remarks
In addition to producing excellent interpolating curves, cubic splines and their generalizations are useful for numerical integration
and differentiation, for the numerical solution of differential and integral equations, and in optimization theory.
Exercise Set 11.5
Click here for Just Ask!
Derive the expressions for and in Equations 14 of Theorem 11.5.1.
1.
The six points
2.