Page 103 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp
P. 103
Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics
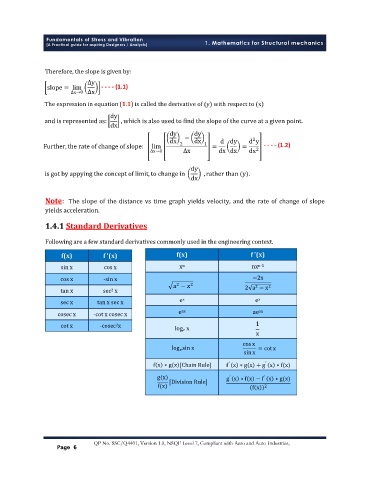
ǡ ǣ
∆y
slope = lim - - - - (1.1)
∆x→0 ∆x
The expression in equation (ͳǤͳ) is called the derivative of (y) with respect to (x)
dy
and is represented as: , which is also used to find the slope of the curve at a given point.
dx
dy dy
−
2
dx dx d dy d y
Further, the rate of change of slope: lim 2 1 = = - - - - (1.2)
∆x→0 ∆x dx dx dx 2
dy
is got by appying the concept of limit, to change in , rather than (y).
dx
ǣ
ǡ
Ǥ
ͳǤͶǤͳ
Ǥ
ȋȌ ǯȋȌ ȋȌ ǯȋȌ
-ͳ
- −2x
a − x 2 2
2
2
2 a − x
ʹ
-
-
1
ʹ
x
cos x
log sin x = cot x
e
sin x
′
f x ∗ g x [Chain Rule] f x ∗ g x + g x ∗ f(x)
′
g(x) g x ∗ f x − f x ∗ g(x)
′
′
f(x) [Division Rule] (f(x)) 2
QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 6