Page 105 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics
2
šƒ’Ž‡ ͳǣ ϐ‹† –Š‡ ƒš ‘” ‹ ˜ƒŽ—‡ ˆ‘” –Š‡ ˆ— –‹‘ [y = 4x + 2x − 16] - - - - (1.3)

‘Ž—–‹‘ ͳǣ

dy
Differentiating y , and equating the slope to zero, we get: = 8x + 2 = 0
dx
2
Therefore, we have x = − = −0.25
8

‘™ǡ –‘ —†‡”•–ƒ† ‹ˆ ƒ ‹‹— ‘” ƒš‹— ‡š‹•–• ƒ– ȋš α -ͲǤʹͷȌǡ Ž‡– —• ‘’—–‡ ‹ˆ –Š‡ ”ƒ–‡ ‘ˆ
Šƒ‰‡ ‘ˆ •Ž‘’‡ ‹• ’‘•‹–‹˜‡ ‘” ‡‰ƒ–‹˜‡Ǥ
2
d y
Rate of change of slope = = 8
dx 2
2
d y
Since the rate of change of slope is positive > 0 , y assumes a minimum value.
dx 2
Š‡ ˜ƒŽ—‡ ‘ˆ ȋ›Ȍ ‹• ‰‘– „› •—„•–‹–—–‹‰ –Š‡ ˜ƒŽ—‡ ‘ˆ ȋšȌ ‹ ‡“—ƒ–‹‘ ȋͳǤ͵Ȍ

2
That is: y = 4 0.25 + 2 ∗ −0.25 − 16 = −16.25
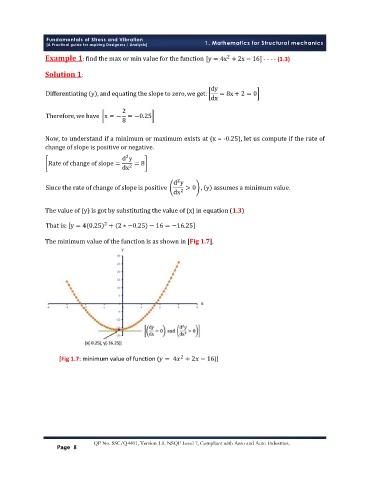
Š‡ ‹‹— ˜ƒŽ—‡ ‘ˆ –Š‡ ˆ— –‹‘ ‹• ƒ• •Š‘™ ‹ ȏ ‹‰ ͳǤ͹ȐǤ

[Fig 1.7: minimum value of function ( = 4 + 2 − 16)]
2

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 8