Page 191 - Fisika Dasar 1 - Mikrajuddin Abdullah

Bab 3 Gerak Dua Dimensi

gX s  x   1 x 2  v s  

2v 2 0   v 0  

atau

X s  x   1 x 2  v s  (3.22)


2R maks   v 0 

di mana Rmaks diberikan oleh persamaan (3.13).

Persamaan (3.22) dapat diseselaikan secara numerik jika kita
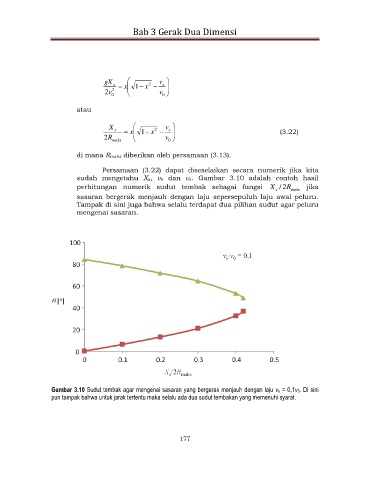
sudah mengetahu Xs, v0 dan vs. Gambar 3.10 adalah contoh hasil
perhitungan numerik sudut tembak sebagai fungsi X / 2 R maks jika
s
sasaran bergerak menjauh dengan laju sepersepuluh laju awal peluru.
Tampak di sini juga bahwa selalu terdapat dua pilihan sudut agar peluru
mengenai sasaran.

Gambar 3.10 Sudut tembak agar mengenai sasaran yang bergerak menjauh dengan laju vs = 0,1v0. Di sini
pun tampak bahwa untuk jarak tertentu maka selalu ada dua sudut tembakan yang memenuhi syarat.

177