Page 37 - Fisika Terapan for Engineers and Scientists

8.1 Potential Energy of a Conservative Force 237

then the work is, indeed, the difference between two potential energies
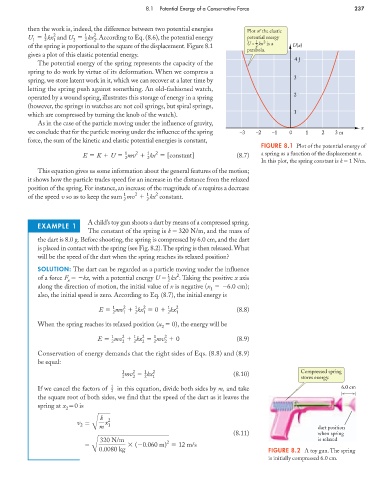
Plot of the elastic
U 1 kx 2 and U 1 kx 2 . According to Eq. (8.6), the potential energy potential energy
1 2 1 2 2 2 1 2
of the spring is proportional to the square of the displacement. Figure 8.1 U = kx is a U (x)
2
parabola.
gives a plot of this elastic potential energy.
4 J
The potential energy of the spring represents the capacity of the
spring to do work by virtue of its deformation. When we compress a
3
spring, we store latent work in it, which we can recover at a later time by
letting the spring push against something. An old-fashioned watch,
operated by a wound spring, illustrates this storage of energy in a spring 2
(however, the springs in watches are not coil springs, but spiral springs,
which are compressed by turning the knob of the watch). 1
As in the case of the particle moving under the influence of gravity,
x
we conclude that for the particle moving under the influence of the spring –3 –2 –1 0 1 2 3 m
force, the sum of the kinetic and elastic potential energies is constant,
FIGURE 8.1 Plot of the potential energy of
1
1
2
2
E K U mv kx [constant] (8.7) a spring as a function of the displacement x.
2
2
In this plot, the spring constant is k 1 N/m.
This equation gives us some information about the general features of the motion;
it shows how the particle trades speed for an increase in the distance from the relaxed
position of the spring. For instance, an increase of the magnitude of x requires a decrease
1
2
of the speed v so as to keep the sum mv 1 2 kx 2 constant.
2
A child’s toy gun shoots a dart by means of a compressed spring.
EXAMPLE 1
The constant of the spring is k 320 N/m, and the mass of
the dart is 8.0 g. Before shooting, the spring is compressed by 6.0 cm, and the dart
is placed in contact with the spring (see Fig. 8.2).The spring is then released.What
will be the speed of the dart when the spring reaches its relaxed position?
SOLUTION: The dart can be regarded as a particle moving under the influence
of a force F kx, with a potential energy U 1 2 kx 2 . Taking the positive x axis
x
along the direction of motion, the initial value of x is negative (x 6.0 cm);
1
also, the initial speed is zero. According to Eq. (8.7), the initial energy is
2
2
1
1
1
E mv kx 0 kx 2 1 (8.8)
1
2
1
2
2
When the spring reaches its relaxed position (x 0), the energy will be
2
2
1
2
2
1
1
E mv kx mv 0 (8.9)
2
2
2
2
2
2
Conservation of energy demands that the right sides of Eqs. (8.8) and (8.9)
be equal:
1 2 1 2 Compressed spring
2 mv kx 1 (8.10) stores energy.
2
2
1
If we cancel the factors of in this equation, divide both sides by m, and take 6.0 cm
2
the square root of both sides, we find that the speed of the dart as it leaves the
spring at x 0 is
2
k 2
v x
2 B m 1 dart position
(8.11) when spring
320 N/m 2 is relaxed
( 0.060 m) 12 m/s
B0.0080 kg FIGURE 8.2 A toy gun. The spring
is initially compressed 6.0 cm.