Page 41 - Fisika Terapan for Engineers and Scientists

8.1 Potential Energy of a Conservative Force 241

(a) (b)
U
U
0 1 2 3 4 m
x
1 J For repulsive force,
dU/dx is negative.
1
– J
3 4
4
– 1
1 2
2
1 – 3 4
4 For attractive force,
dU/dx is positive.
–1
x
0 1 2 3 4 m
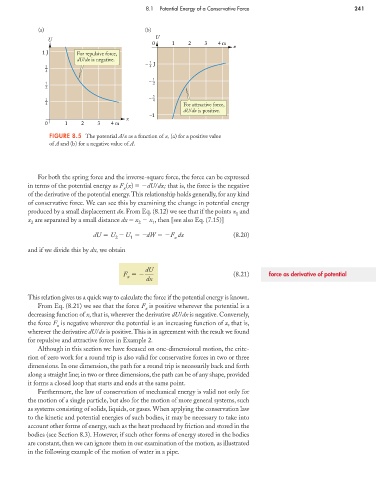
FIGURE 8.5 The potential A/x as a function of x, (a) for a positive value
of A and (b) for a negative value of A.

For both the spring force and the inverse-square force, the force can be expressed
in terms of the potential energy as F (x) dU/dx; that is, the force is the negative
x
of the derivative of the potential energy.This relationship holds generally, for any kind
of conservative force. We can see this by examining the change in potential energy
produced by a small displacement dx. From Eq. (8.12) we see that if the points x and
1
x are separated by a small distance dx x x , then [see also Eq. (7.15)]
2 2 1
dU U U dW F dx (8.20)
2
x
1

and if we divide this by dx, we obtain
dU
F (8.21) force as derivative of potential
x
dx
This relation gives us a quick way to calculate the force if the potential energy is known.
From Eq. (8.21) we see that the force F is positive wherever the potential is a
x
decreasing function of x, that is, wherever the derivative dU/dx is negative. Conversely,
the force F is negative wherever the potential is an increasing function of x, that is,
x
wherever the derivative dU/dx is positive.This is in agreement with the result we found
for repulsive and attractive forces in Example 2.
Although in this section we have focused on one-dimensional motion, the crite-
rion of zero work for a round trip is also valid for conservative forces in two or three
dimensions. In one dimension, the path for a round trip is necessarily back and forth
along a straight line; in two or three dimensions, the path can be of any shape, provided
it forms a closed loop that starts and ends at the same point.
Furthermore, the law of conservation of mechanical energy is valid not only for
the motion of a single particle, but also for the motion of more general systems, such
as systems consisting of solids, liquids, or gases. When applying the conservation law
to the kinetic and potential energies of such bodies, it may be necessary to take into
account other forms of energy, such as the heat produced by friction and stored in the
bodies (see Section 8.3). However, if such other forms of energy stored in the bodies
are constant, then we can ignore them in our examination of the motion, as illustrated
in the following example of the motion of water in a pipe.