Page 73 - Fisika Terapan for Engineers and Scientists

9.1 Newton’s Law of Universal Gravitation 273

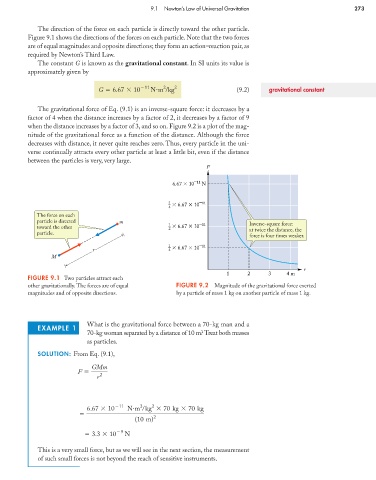
The direction of the force on each particle is directly toward the other particle.
Figure 9.1 shows the directions of the forces on each particle. Note that the two forces
are of equal magnitudes and opposite directions; they form an action–reaction pair, as
required by Newton’s Third Law.
The constant G is known as the gravitational constant. In SI units its value is
approximately given by

2
G 6.67 10 11 N m /kg 2 (9.2) gravitational constant

The gravitational force of Eq. (9.1) is an inverse-square force: it decreases by a
factor of 4 when the distance increases by a factor of 2, it decreases by a factor of 9
when the distance increases by a factor of 3, and so on. Figure 9.2 is a plot of the mag-
nitude of the gravitational force as a function of the distance. Although the force
decreases with distance, it never quite reaches zero. Thus, every particle in the uni-
verse continually attracts every other particle at least a little bit, even if the distance
between the particles is very, very large.
F

6.67 10 –11 N

3 6.67 10 –11
4
The force on each
particle is directed m Inverse-square force:
toward the other 1 2 6.67 10 –11 at twice the distance, the
particle.
force is four times weaker.
1 6.67 10 –11
r 4
M
r
1 2 3 4 m
FIGURE 9.1 Two particles attract each
other gravitationally. The forces are of equal FIGURE 9.2 Magnitude of the gravitational force exerted
magnitudes and of opposite directions. by a particle of mass 1 kg on another particle of mass 1 kg.

What is the gravitational force between a 70-kg man and a
EXAMPLE 1
70-kg woman separated by a distance of 10 m? Treat both masses
as particles.
SOLUTION: From Eq. (9.1),
GMm
F
r 2

11 2 2
6.67 10 N m /kg 70 kg 70 kg

(10 m) 2
3.3 10 9 N

This is a very small force, but as we will see in the next section, the measurement
of such small forces is not beyond the reach of sensitive instruments.