Page 24 - mathsvol1ch1to3ans

24

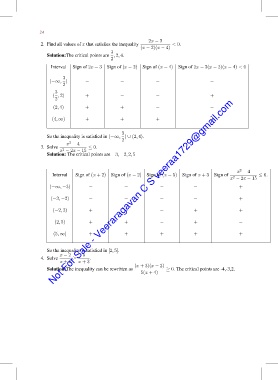
2x − 3
2. Find all values of x that satisfies the inequality < 0.
(x − 2)(x − 4)
3
Solution:The critical points are , 2, 4.
2

Interval Sign of 2x − 3 Sign of (x − 2) Sign of (x − 4) Sign of 2x − 3(x − 2)(x − 4) < 0

3
(−∞, ) − − − −
2
3
( , 2) + − − +
2
Not For Sale - Veeraragavan C S veeraa1729@gmail.com
(2, 4) + + − −

(4, ∞) + + + +

3
So the inequality is satisfied in (−∞, ) ∪ (2, 4).
2
2
x − 4
3. Solve ≤ 0.
2
x − 2x − 15
Solution: The critical points are −3, −2, 2, 5

2
x − 4
Interval Sign of (x + 2) Sign of (x − 2) Sign of (x − 5) Sign of x + 3 Sign of ≤ 0.
2
x − 2x − 15
(−∞, −3) − − − − +

(−3, −2) − − − − +

(−2, 2) + − − + +

(2, 5) + + − + −

(5, ∞) + + + + +

So the inequality is satisfied in [2, 5].
x − 2 5
4. Solve ≥ .
x + 4 x + 3
(x + 3)(x − 2)
Solution:The inequality can be rewritten as ≥ 0. The critical points are -4,-3,2.
5(x + 4)