Page 13 - fiches-revision_2018

FICHES DE REVISION BAC 2018

LE DIPÔLE RC

 Équation différentielle :

Attention : on doit représenter les flèches des tensions avant d’établir l’équation différentielle.
u u - u = 0 donc :
R c G
du
RC C  u E équation différentielle
dt C
de lach arge d 'un condensateur en u C

 Solution de l’équation différentielle :
* La solution de l 'équation différentielle s 'écrit u C   A Be  t
( ,A B et  des cons tantes positives )
*A t  0;u C ( ) 0 ( o le condensateur est initialement vide )
 A  Be 0  0 B  A d 'ou u C  A  Ae  t
du
*cette solution vérifie l 'équation différentielle :RC C  u E
dt C
RC (0  Ae   )  A  Ae  t  t  E
RC Ae  t  A  Ae  t  0  Ae  t (RC  1)  A  E ;
  t 1 1
RC  1  0 car A .e  0 d 'ou   
 RC 
 A  E

t t
 
u C  E  Ee   E (1e  )

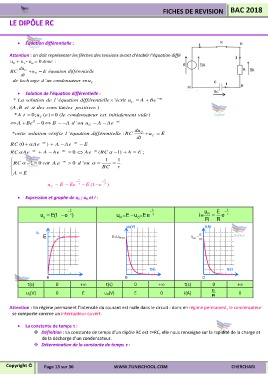
 Expression et graphe de u C ; u R et i :

 t  t u E  t
u  E(1 e )  u =E u =Ee  i= R  e

c R C
R R
u R(V) i(A)
u c E
E E=U Rmax I max  R

E t(s) t(s)
0 X 0 0
t(s) 0 + t(s) 0 + t(s) 0 +
E
u c(V) 0 E u R(V) E 0 i(A) E 0
R R
C
Attention : En régime permanent l’intensité du courant est nulle dans le circuit : donc en régime permanent, le condensateur
I
se comporte comme un interrupteur ouvert.
C
 La constante de temps  :
E
 Définition : La constante de temps d’un dipôle RC est =RC, elle nous renseigne sur la rapidité de la charge et
S
de la décharge d’un condensateur.

 Détermination de la constante de temps  :
D
E
Copyright © Page 13 sur 36 WWW.TUNISCHOOL.COM CHERCHARI

S