Page 17 - fiches-revision_2018

FICHES DE REVISION BAC 2018

LE DIPÔLE RLC EN REGIME AMORTI

 Équation différentielle
D’après la loi des mailles(K est en position 2) :
2
di d q (R r) dq q
u B + u R + u C =0 L  ri Ri u   0     0
dt c dt 2 L dt LC
 Non conservation de l’énergie totale d’un circuit RLC série
1 1
L’énergie totale E = E c + E L = cu 2  Li .
2
2 c 2
dE
On trouve :  i( (R r)i)   (R r)i 2
dt
dE  0 donc Eestdécroissante.L’énergie totale d’un circuit RLC série diminue au cours du temps à cause de
dt
l’énergie dissipée par effet joule dans les résistances.
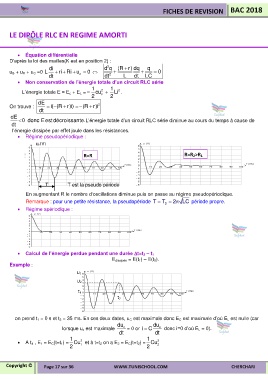
 Régime pseudopériodique :
u c (V)

R=R R=R 2>R 1

1

T T est la pseudo période

En augmentant R le nombre d’oscillations diminue puis on passe au régime pseudopériodique.
Remarque : pour une petite résistance, la pseudopériode T  T  2 LC période propre.
0
 Régime apériodique :

 Calcul de l’énergie perdue pendant une durée t=t 2 – t 1
E dissipée = E(t 1) – E(t 2).
Exemple :

u 1

u 2

t 1
t 2

on prend t 1 = 0 s et t 2 = 35 ms. En ces deux dates, u C est maximale donc E C est maximale d’où E L est nulle (car
du du
lorsque u c est maximale c = 0 or i C c donc i=0 d’où E L = 0).
dt dt
1 1
2
2
 A t 1 , E 1 = E C(t=t 1) = Cu et à t=t 2 on a E 2 = E C(t=t 2) = Cu
2
1
2 2
Copyright © Page 17 sur 36 WWW.TUNISCHOOL.COM CHERCHARI