Page 108 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

84 ERRORES DE TRUNCAMIENTO Y LA SERIE DE TAYLOR

Sin embargo, observe también que la mejor aproximación se consigue con los primeros
–2
términos. En este caso, al agregar el tercer término, el error se redujo al 2.62 × 10 %, lo
cual significa que se alcanzó el 99.9738% del valor exacto. Por consiguiente, aunque se
le agreguen más términos a la serie el error decrece, aunque la mejoría será mínima.

4.1.1 El residuo en la expansión de la serie de Taylor

Antes de mostrar cómo se utiliza la serie de Taylor en la estimación de errores numéri-
cos, se debe explicar por qué se incluye el argumento x en la ecuación (4.8). Un desarro-
llo matemático se presenta en el cuadro 4.1. Ahora se expondrá una interpretación más
visual. Después se extiende este caso específico a una formulación más general.
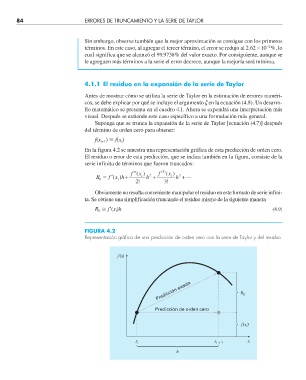
Suponga que se trunca la expansión de la serie de Taylor [ecuación (4.7)] después
del término de orden cero para obtener:
f(x ) f(x )
i+1
i
En la figura 4.2 se muestra una representación gráfica de esta predicción de orden cero.
El residuo o error de esta predicción, que se indica también en la figura, consiste de la
serie infinita de términos que fueron truncados:
x
f x h +
2
i
3
i
R = ′() f ′′() h + f 3 () x () h +
i
0
2! 3!
Obviamente no resulta conveniente manipular el residuo en este formato de serie infini-
ta. Se obtiene una simplificación truncando el residuo mismo de la siguiente manera
R f′(x )h (4.9)
0
i
FIGURA 4.2
Representación gráfi ca de una predicción de orden cero con la serie de Taylor y del residuo.
f (x)

Predicción exacta R 0

Predicción de orden cero

f(x )
i

x x x
i i +1
h

6/12/06 13:44:42
Chapra-04.indd 84 6/12/06 13:44:42
Chapra-04.indd 84