Page 583 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

19.6 TRANSFORMADA RÁPIDA DE FOURIER 559

2 000

2
TDF(N )
Operaciones 1 000

N
TRF(N log 2

0 40
Muestras

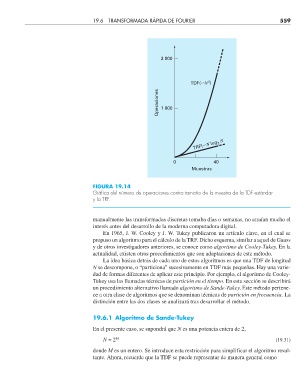
FIGURA 19.14
Gráfi ca del número de operaciones contra tamaño de la muestra de la TDF estándar
y la TRF.

manualmente las transformadas discretas tomaba días o semanas, no atraían mucho el
interés antes del desarrollo de la moderna computadora digital.
En 1965, J. W. Cooley y J. W. Tukey publicaron un artículo clave, en el cual se
propuso un algoritmo para el cálculo de la TRF. Dicho esquema, similar a aquel de Gauss
y de otros investigadores anteriores, se conoce como algoritmo de Cooley-Tukey. En la
actualidad, existen otros procedimientos que son adaptaciones de este método.
La idea básica detrás de cada uno de estos algoritmos es que una TDF de longitud
N se descompone, o “particiona” sucesivamente en TDF más pequeñas. Hay una varie-
dad de formas diferentes de aplicar este principio. Por ejemplo, el algoritmo de Cooley-
Tukey usa las llamadas técnicas de partición en el tiempo. En esta sección se describirá
un procedimiento alternativo llamado algoritmo de Sande-Tukey. Este método pertene-
ce a otra clase de algoritmos que se denominan técnicas de partición en frecuencia. La
distinción entre las dos clases se analizará tras desarrollar el método.

19.6.1 Algoritmo de Sande-Tukey
En el presente caso, se supondrá que N es una potencia entera de 2,

N = 2 M (19.31)
donde M es un entero. Se introduce esta restricción para simplificar el algoritmo resul-
tante. Ahora, recuerde que la TDF se puede representar de manera general como

6/12/06 13:58:24
Chapra-19.indd 559 6/12/06 13:58:24
Chapra-19.indd 559