Page 580 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

556 APROXIMACIÓN DE FOURIER

Ahora que se ha presentado una forma para analizar una señal no periódica, veremos
el paso final en nuestro desarrollo. En la siguiente sección analizaremos el hecho de que
una señal rara vez está caracterizada como una función continua que se necesita para
implementar la ecuación (19.26). En lugar de esto, los datos invariablemente están en
forma discreta. Ahora se mostrará cómo calcular la transformada de Fourier a partir de
mediciones discretas.

19.5 TRANSFORMADA DISCRETA DE FOURIER (TDF)

En ingeniería, las funciones en general se representan por conjuntos finitos de valores
discretos. Es decir, los datos con frecuencia se obtienen de, o convierten a, una forma
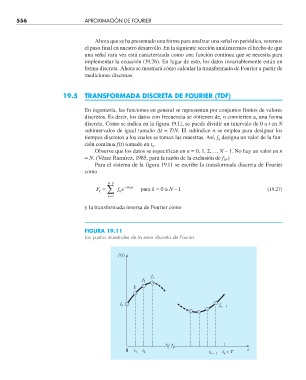
discreta. Como se indica en la figura 19.11, se puede dividir un intervalo de 0 a t en N
subintervalos de igual tamaño ∆t = T/N. El subíndice n se emplea para designar los
tiempos discretos a los cuales se toman las muestras. Así, f designa un valor de la fun-
n
ción continua f(t) tomado en t .
n
Observe que los datos se especifican en n = 0, 1, 2,…, N – 1. No hay un valor en n
= N. (Véase Ramírez, 1985, para la razón de la exclusión de f .)
N
Para el sistema de la figura 19.11 se escribe la transformada discreta de Fourier
como

k ∑
F = N−1 f e i − ω 0 n para k = 0 a N −1 (19.27)
n
n=0
y la transformada inversa de Fourier como

FIGURA 19.11
Los puntos muestrales de la serie discreta de Fourier.

f (t)

f
f 2 3
f 1

f 0 f n –1

0 t 1 t 2 t n –1 t = T t
n

6/12/06 13:58:24
Chapra-19.indd 556
Chapra-19.indd 556 6/12/06 13:58:24