Page 743 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

CAPÍTULO 25

Métodos de Runge-Kutta

Este capítulo se dedica a la solución de ecuaciones diferenciales ordinarias de la forma
dy
= fx y(, )
dx
En el capítulo 1 se utilizó un método numérico para resolver una ecuación como la an-
terior, para el cálculo de la velocidad del paracaidista en caída. Recuerde que el método
fue de la forma general

Nuevo valor = valor anterior + pendiente × tamaño de paso
o, en términos matemáticos,

y = y + fh (25.1)
i+1
i
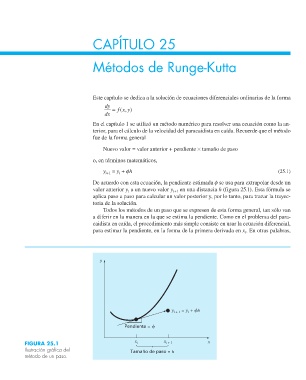
De acuerdo con esta ecuación, la pendiente estimada f se usa para extrapolar desde un
valor anterior y i a un nuevo valor y i+1 en una distancia h (figura 25.1). Esta fórmula se
aplica paso a paso para calcular un valor posterior y, por lo tanto, para trazar la trayec-
toria de la solución.
Todos los métodos de un paso que se expresen de esta forma general, tan sólo van
a diferir en la manera en la que se estima la pendiente. Como en el problema del para-
caidista en caída, el procedimiento más simple consiste en usar la ecuación diferencial,
para estimar la pendiente, en la forma de la primera derivada en x i . En otras palabras,

y

y i +1 = y + h
i

Pendiente =

FIGURA 25.1 x i x i +1 x
Ilustración gráfi ca del Tamaño de paso = h
método de un paso.

6/12/06 14:01:55
Chapra-25.indd 719
Chapra-25.indd 719 6/12/06 14:01:55