Page 62 - analysis-and-interpretation-of-astronomical-sp

Analysis and Interpretation of Astronomical Spectra 62

15 The Measurement of the Radial Velocity

15.1 The Radial Velocity
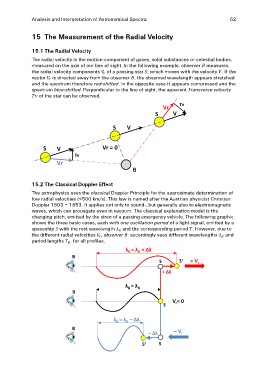
The radial velocity is the motion-component of gases, solid substances or celestial bodies,
measured on the axis of our line of sight. In the following example, observer measures,
the radial velocity components of a passing star , which moves with the velocity . If the
vector is directed away from the observer , the observed wavelength appears stretched
and the spectrum therefore red-shifted. In the opposite case it appears compressed and the
spectrum blue-shifted. Perpendicular to the line of sight, the apparent Transverse velocity

of the star can be observed.

Vr Tv
SV

SV

SV Tv Vr = 0
Vr B

15.2 The Classical Doppler Effect

The astrophysics uses the classical Doppler Principle for the approximate determination of
low radial velocities (<500 km/s). This law is named after the Austrian physicist Christian
Doppler 1803 – 1853. It applies not only to sound-, but generally also to electromagnetic
waves, which can propagate even in vacuum. The classical explanation model is the
changing pitch, emitted by the siren of a passing emergency vehicle. The following graphic
shows the three basic cases, each with one oscillation period of a light signal, emitted by a
spaceship with the rest wavelength and the corresponding period . However, due to
the different radial velocities , observer accordingly sees different wavelengths and
period lengths . for all profiles.

λB = λ0 + Δλ

B

S S‘ + Vr

+ Δλ

λB = λ0

B

S Vr= 0

λB = λ0 – Δλ
B – Δλ – Vr

S‘ S