Page 47 - ArithBook5thEd ~ BCC

Since the area of a right triangle is exactly half the area of the rectangle it came from, it follows
that the area of a right triangle is the product of the lengths of the legs, divided by 2. If A
denotes the area, and the lengths of the legs are a and b as in the figure, the formula is

A =(a · b) ÷ 2.

Example 38. Find the area and perimeter of a triangle whose legs have length 3 feet and 4 feet.

Solution. Putting a =4 and b = 3, we find the area using the formula

2
A =(a · b) ÷ 2= (4 · 3) ÷ 2= 12 ÷ 2= 6 ft .
To find the perimeter, we first find the length of the hypotenuse using the formula

√ √
! !
2
2
2
2
c = a + b = 4 +3 = 16 + 9 = 25 = 5 ft.
Thus the perimeter is a + b + c =4 ft +3 ft +5 ft =12 ft.
Now we can find the area and perimeter of any polygon that can be divided up into rectangles and
right triangles.
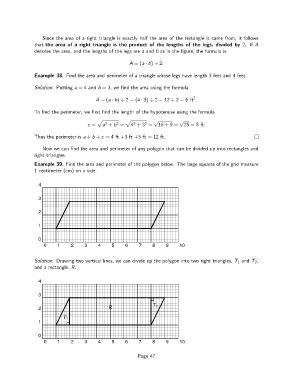
Example 39. Find the area and perimeter of the polygon below. The large squares of the grid measure
1centimeter (cm) on a side.

4

3

2

1

0
0 1 2 3 4 5 6 7 8 9 10

Solution. Drawing two vertical lines, we can divide up the polygon into two right triangles, T 1 and T 2 ,
and a rectangle, R.

4

3

2 R T 2

T 1
1

0
0 1 2 3 4 5 6 7 8 9 10

Page 47