Page 113 - Matematik_Tingkatan_2

Bab 6 Bentuk Geometri Tiga Dimensi Bab 6 Bentuk Geometri Tiga Dimensi

JOM CUBA 6.2 Piramid

1. Dengan menggunakan kertas grid 1 cm persegi, lukis bentangan dan bina model setiap bentuk × luas segi empat sama +
tiga dimensi berikut.
2 cm
(a) 2 cm (b) (c) (d) × luas segi tiga
10 cm 5 cm
4 cm 4 cm Prisma
8 cm 4 cm 6 cm × luas segi tiga +
7 cm 5 cm 6 cm
6 cm
t × luas segi empat
2. Nyatakan bentuk tiga dimensi yang boleh dibina daripada bentangan berikut.
Bina model sebenar. Silinder
(a) (b) (c) (d) × luas bulatan +
7 cm
8 cm
× luas segi empat tepat

Kon
BAB 6 7 cm 6 cm 5 cm 5 cm s × luas bulatan + BAB 6
7 cm

5 cm
× luas permukaan melengkung
6.3 Luas Permukaan Bentuk Tiga Dimensi
Perbincangan:
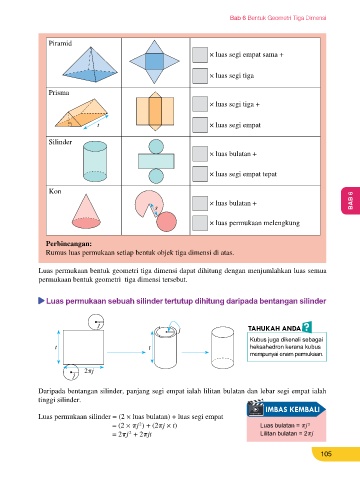
6.3.1 Luas permukaan kubus, kuboid, piramid, Rumus luas permukaan setiap bentuk objek tiga dimensi di atas.
prisma, silinder dan kon
Menerbitkan rumus luas Luas permukaan bentuk geometri tiga dimensi dapat dihitung dengan menjumlahkan luas semua
permukaan kubus, kuboid, permukaan bentuk geometri tiga dimensi tersebut.
piramid, prisma, silinder
dan kon, dan seterusnya
Tujuan: Menentukan luas permukaan bentuk geometri tiga dimensi menentukan luas permukaan Luas permukaan sebuah silinder tertutup dihitung daripada bentangan silinder
Bahan: Lembaran kerja bentuk tersebut.
Langkah:
Isi petak kosong dengan bilangan muka setiap bentuk geometri tiga dimensi berikut. j
j
Bentuk Bentangan Luas Permukaan Kubus juga dikenali sebagai
Kubus t t heksahedron kerana kubus
mempunyai enam permukaan.
× luas segi empat sama 2πj
j
Kuboid Daripada bentangan silinder, panjang segi empat ialah lilitan bulatan dan lebar segi empat ialah
tinggi silinder.
× luas segi empat tepat +
Luas permukaan silinder = (2 × luas bulatan) + luas segi empat
× luas segi empat sama = (2 × πj ) + (2πj × t) Luas bulatan = πj 2
2
2
= 2πj + 2πjt Lilitan bulatan = 2πj
104 105