Page 208 - Matematik_Tingkatan_2

Bab 10 Kecerunan Garis Lurus Bab 10 Kecerunan Garis Lurus

4. Nyatakan jarak mencancang dan jarak mengufuk bagi pasangan titik yang diberikan.
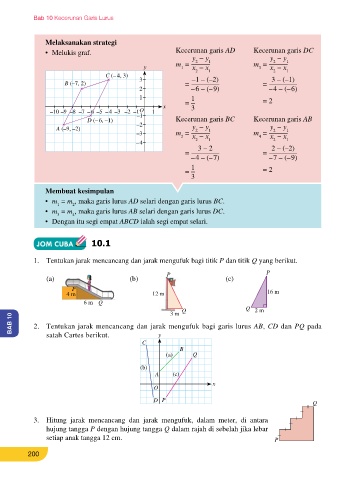
Melaksanakan strategi
• Melukis graf. Kecerunan garis AD Kecerunan garis DC (a) (3, 0) dan (−2, 6) (b) (1, 1) dan (6, 5) (c) (3, 1) dan (1, 5)
y − y 1 y − y 1
2
2
y m = x − x 1 m = x − x 1 (d) (0, 0) dan (4, 4) (e) (1, −2) dan (2, 4) (f) (3, 6) dan (6, −3)
1
3
2
2
C (– 4, 3)
B (–7, 2) 3 = –1 – (–2) = 3 – (–1)
2 – 6 – (– 9) – 4 – (– 6) 5. Nyatakan nilai pintasan-x dan nilai pintasan-y bagi garis lurus AB.
1 1 = 2 (a) y (b) y (c) y (d) y
x = 3 B A
O
–10 –9 –8 –7 – 6 –5 – 4 –3 –2 –1 –1 1 A B
D (– 6, –1) Kecerunan garis BC Kecerunan garis AB 4 −6 O 3 x 3 −1 O x
A (–9, –2) –2 y − y 1 y − y 1
2
2
–3 m = m =
2 x − x 4 x − x –2
– 4 2 1 2 1 O 8 B x −7 O x
= 3 – 2 = 2 – (–2) A −5 B
– 4 – (– 7) – 7 – (– 9) A
1 6. Kenal pasti garis lurus yang mempunyai kecerunan terbesar dalam setiap rajah di bawah.
= = 2
3 (a) y (b) y
Membuat kesimpulan A F
• m = m , maka garis lurus AD selari dengan garis lurus BC.
1 2 D D
• m = m , maka garis lurus AB selari dengan garis lurus DC.
3 4 C F
• Dengan itu segi empat ABCD ialah segi empat selari. E A
E x x
O O B
10.1 B C

1. Tentukan jarak mencancang dan jarak mengufuk bagi titik P dan titik Q yang berikut. 7. Berdasarkan rajah berikut, nyatakan kecerunan y

P P sama ada positif atau negatif.
(a) (b) (c) (a) LM 8 N
P (b) MN
4 m 12 m 16 m 6
6 m Q Q Q 2 m (c) NO 4 L O
(d) OQ
3 m
BAB 10 2. Tentukan jarak mencancang dan jarak mengufuk bagi garis lurus AB, CD dan PQ pada 2 M Q BAB 10
satah Cartes berikut.
C y O 2 4 6 8 10 x
B
(a) Q 8. Hitung kecerunan garis lurus dalam setiap rajah yang berikut.
(b) (a) (b) (c) 2 unit
A (c)
x 7 unit
O
100 cm 12 cm
D P Q

3. Hitung jarak mencancang dan jarak mengufuk, dalam meter, di antara
hujung tangga P dengan hujung tangga Q dalam rajah di sebelah jika lebar 50 cm
setiap anak tangga 12 cm. P 3 cm

200 201