Page 86 - Matematik Tambahan Tingkatan 5 KSSM

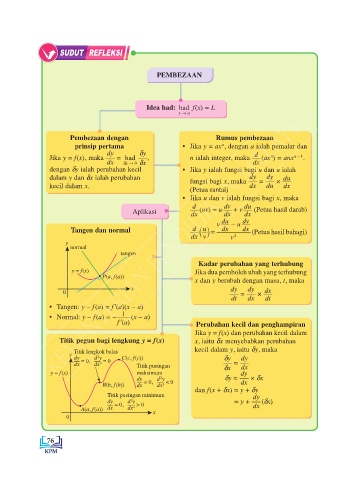
SUDUT REFLEKSI

PEMBEZAAN

KEMENTERIAN PENDIDIKAN MALAYSIA
Idea had: had f(x) = L

x ˜ a

Pembezaan dengan Rumus pembezaan
n
prinsip pertama • Jika y = ax , dengan a ialah pemalar dan
dy dy d
n

Jika y = f(x), maka = had , n ialah integer, maka (ax ) = anx n – 1 .
dx dx ˜ 0 dx dx
dengan dy ialah perubahan kecil • Jika y ialah fungsi bagi u dan u ialah
dalam y dan dx ialah perubahan fungsi bagi x, maka dy = dy × du
kecil dalam x. dx du dx
(Petua rantai)
• Jika u dan v ialah fungsi bagi x, maka
d dv du
Aplikasi dx (uv) = u dx + v dx (Petua hasil darab)
du dv
v – u
( )
Tangen dan normal d u = dx dx (Petua hasil bahagi)

dx v v 2
y
normal
tangen
Kadar perubahan yang terhubung
y = f(x) Jika dua pemboleh ubah yang terhubung
P(a, f(a))
x dan y berubah dengan masa, t, maka
x dy dy
0 = × dx
dt dx dt
• Tangen: y – f (a) = f (a)(x – a)
• Normal: y – f (a) = – 1 (x – a)
f (a) Perubahan kecil dan penghampiran

Jika y = f(x) dan perubahan kecil dalam
Titik pegun bagi lengkung y = f(x) x, iaitu dx menyebabkan perubahan

Titik lengkok balas kecil dalam y, iaitu dy, maka
y
dy d y = 0 C(c, f(c)) dy dy
2
dx dx Titik pusingan dx ≈ dx
–– = 0, –– 2
y = f(x) maksimum dy
2
dy d y dy ≈ × dx
B(b, f(b)) –– = 0, –– 2 < 0 dx
dx
dx

dan f(x + dx) ≈ y + dy
Titik pusingan minimum dy
dy d y > 0 ≈ y + (dx)
2
–– = 0, –– 2
A(a, f(a)) dx dx dx
x
0
76