Page 200 - Matematik Tambahan Tingkatan 4 KSSM

7.3 Luas Poligon

Menerbitkan rumus luas segi tiga

Dalam satah Cartes, apabila bucu-bucu suatu poligon diketahui, kita boleh menggunakan
rumus untuk mencari luasnya. Ikuti penerokaan berikut untuk menerbitkan rumus luas suatu
segi tiga apabila koordinat setiap bucunya diketahui.

Inkuiri 3 Berkumpulan PAK-21
Tujuan: Menentukan luas segi tiga apabila koordinat setiap bucu diketahui
Arahan:
1. Dengan menggunakan perisian GeoGebra, lukis sebuah segi tiga dengan bucu-bucu
A, B, dan C.
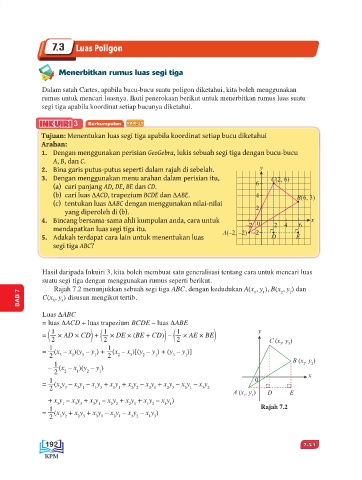
2. Bina garis putus-putus seperti dalam rajah di sebelah. y
3. Dengan menggunakan menu arahan dalam perisian itu, C(2, 6)
(a) cari panjang AD, DE, BE dan CD. 6
(b) cari luas ΔACD, trapezium BCDE dan ΔABE. 4 B(6, 3)
(c) tentukan luas ΔABC dengan menggunakan nilai-nilai
yang diperoleh di (b). 2
4. Bincang bersama-sama ahli kumpulan anda, cara untuk 0 x
mendapatkan luas segi tiga itu. –2 2 4 6
5. Adakah terdapat cara lain untuk menentukan luas A(–2, –2) –2 D E
segi tiga ABC?

Hasil daripada Inkuiri 3, kita boleh membuat satu generalisasi tentang cara untuk mencari luas
suatu segi tiga dengan menggunakan rumus seperti berikut.
Rajah 7.2 menunjukkan sebuah segi tiga ABC, dengan kedudukan A(x , y ), B(x , y ) dan
BAB 7 C(x , y ) disusun mengikut tertib.
1
1
2
2
3
3
Luas ΔABC
= luas ΔACD + luas trapezium BCDE – luas ΔABE
( 1 ) ( 1 ) ( 1 ) y
= 2 × AD × CD + 2 × DE × (BE + CD) – 2 × AE × BE
C (x , y )
3 3
1 1
= (x – x )(y – y ) + (x – x )[(y – y ) + (y – y )]
2 3 1 3 1 2 2 3 2 1 3 1
B (x , y )
1 2 2
– (x – x )(y – y )
2 2 1 2 1
x
1 0
= (x y – x y – x y + x y + x y – x y + x y – x y – x y
2 3 3 3 1 1 3 1 1 2 2 2 1 2 3 2 1 3 2
A (x , y ) D E
1 1
+ x y – x y + x y – x y + x y + x y – x y )
3 1 3 3 3 1 2 2 2 1 1 2 1 1
1 Rajah 7.2
= (x y + x y + x y – x y – x y – x y )
2 1 2 2 3 3 1 2 1 3 2 1 3
192 7.3.1