Page 236 - Matematik Tambahan Tingkatan 4 KSSM

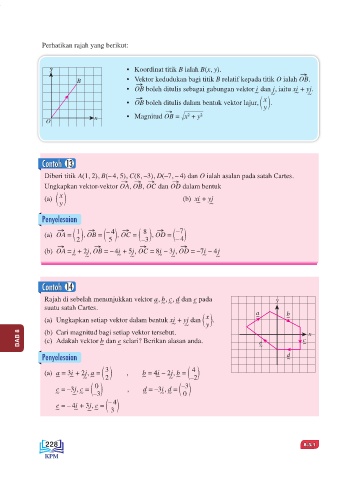
Perhatikan rajah yang berikut:

y • Koordinat titik B ialah B(x, y).
→
B • Vektor kedudukan bagi titik B relatif kepada titik O ialah OB.
→
• OB boleh ditulis sebagai gabungan vektor i dan j, iaitu xi + yj.
∼
∼
∼
∼
→
x
• OB boleh ditulis dalam bentuk vektor lajur, ( ) .
→ y
• Magnitud OB =  2
2
y
+
x
x
O
Contoh 13
Diberi titik A(1, 2), B(– 4, 5), C(8, –3), D(–7, – 4) dan O ialah asalan pada satah Cartes.
→ → → →
Ungkapkan vektor-vektor OA, OB, OC dan OD dalam bentuk
( )
x
(a) (b) xi + yj
∼
y ∼
Penyelesaian
→ 1 → – 4 → 8 → –7
(a) OA = ( ) , OB = ( ) , OC = ( ) , OD = ( )
– 4
5
–3
2
→ → → →
(b) OA = i + 2j, OB = – 4i + 5j, OC = 8i – 3j, OD = –7i – 4j
∼ ∼ ∼ ∼ ∼ ∼ ∼ ∼

Contoh 14

Rajah di sebelah menunjukkan vektor a, b, c, d dan e pada y
∼
∼ ∼ ∼ ∼
suatu satah Cartes.
a b
x
(a) Ungkapkan setiap vektor dalam bentuk xi + yj dan ( ) . ~ ~
∼ ∼ y
BAB 8 (b) Cari magnitud bagi setiap vektor tersebut. e ~ c ~ x
(c) Adakah vektor b dan e selari? Berikan alasan anda.
∼
∼
Penyelesaian d
~
3
4
(a) a = 3i + 2j, a = ( ) , b = 4i – 2j, b = ( )
∼ ∼ ∼ ∼ 2 ∼ ∼ ∼ ∼ –2
0
–3
c = –3j, c = ( ) , d = –3i, d = ( )
∼ ∼ ∼ –3 ∼ ∼ ∼ 0
– 4
e = – 4i + 3j, e = ( )
∼ ∼ ∼ ∼ 3

228 8.3.1