Page 306 - Applied Statistics with R

306 CHAPTER 14. TRANSFORMATIONS

Fitted versus Residuals Normal Q-Q Plot

50000 50000
Residuals 0 Sample Quantiles 0

-50000 -50000

50000 100000 150000 200000 -2 -1 0 1 2
Fitted Theoretical Quantiles

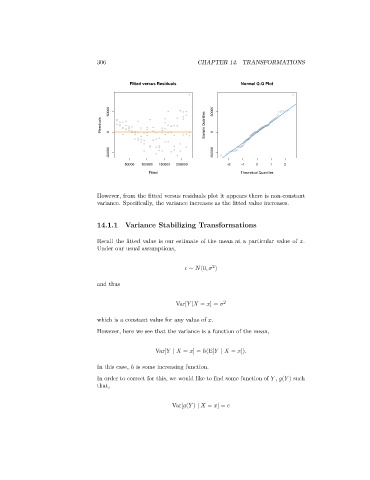
However, from the fitted versus residuals plot it appears there is non-constant
variance. Specifically, the variance increases as the fitted value increases.

14.1.1 Variance Stabilizing Transformations

Recall the fitted value is our estimate of the mean at a particular value of .
Under our usual assumptions,

2
∼ (0, )

and thus

Var[ | = ] = 2

which is a constant value for any value of .

However, here we see that the variance is a function of the mean,

Var[ ∣ = ] = ℎ(E[ ∣ = ]).

In this case, ℎ is some increasing function.
In order to correct for this, we would like to find some function of , ( ) such
that,

Var[ ( ) ∣ = ] =