Page 187 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

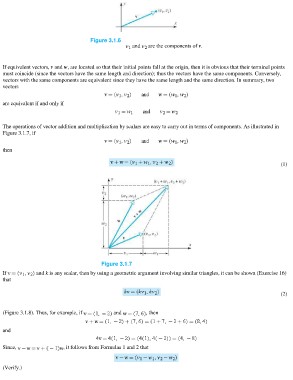
Figure 3.1.6
and are the components of v.

If equivalent vectors, v and w, are located so that their initial points fall at the origin, then it is obvious that their terminal points
must coincide (since the vectors have the same length and direction); thus the vectors have the same components. Conversely,
vectors with the same components are equivalent since they have the same length and the same direction. In summary, two
vectors

are equivalent if and only if

The operations of vector addition and multiplication by scalars are easy to carry out in terms of components. As illustrated in
Figure 3.1.7, if

then

(1)

Figure 3.1.7
If and k is any scalar, then by using a geometric argument involving similar triangles, it can be shown (Exercise 16)
that

(2)

(Figure 3.1.8). Thus, for example, if and , then

and , it follows from Formulas 1 and 2 that
Since,

(Verify.)