Page 70 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition
P. 70
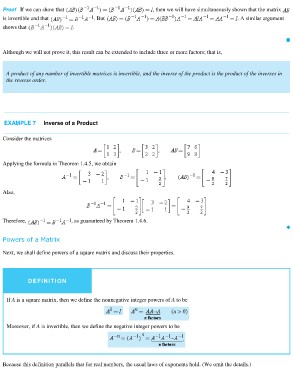
Proof If we can show that . But , then we will have simultaneously shown that the matrix
is invertible and that . A similar argument
shows that
.
Although we will not prove it, this result can be extended to include three or more factors; that is,
A product of any number of invertible matrices is invertible, and the inverse of the product is the product of the inverses in
the reverse order.
EXAMPLE 7 Inverse of a Product
Consider the matrices
Applying the formula in Theorem 1.4.5, we obtain
Also,
Therefore, , as guaranteed by Theorem 1.4.6.
Powers of a Matrix
Next, we shall define powers of a square matrix and discuss their properties.
DEFINITION
If A is a square matrix, then we define the nonnegative integer powers of A to be
Moreover, if A is invertible, then we define the negative integer powers to be
Because this definition parallels that for real numbers, the usual laws of exponents hold. (We omit the details.)