Page 109 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics
1.4.3 Concept of Curvature

The expression for curvature is highly useful, be it, for mechanics of a vehicle negotiating
undulations or curves, or, curvature of a bent beam. Therefore, it is important to derive a
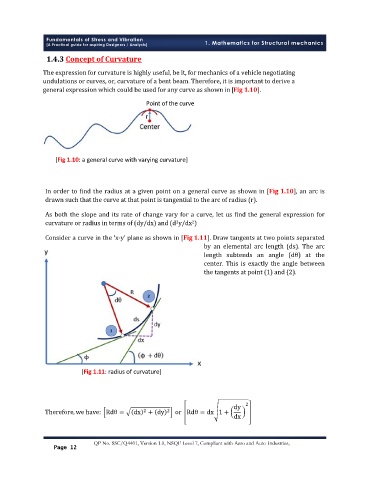
general expression which could be used for any curve as shown in [Fig 1.10].
Point of the curve

[Fig 1.10: a general curve with varying curvature]

 ‘”†‡” –‘ ϐ‹† –Š‡ ”ƒ†‹—• ƒ– ƒ ‰‹˜‡ ’‘‹– ‘ ƒ ‰‡‡”ƒŽ —”˜‡ ƒ• •Š‘™ ‹ ȏ ‹‰ ͳǤͳͲȐǡ ƒ ƒ” ‹•
†”ƒ™ •— Š –Šƒ– –Š‡ —”˜‡ ƒ– –Šƒ– ’‘‹– ‹• –ƒ‰‡–‹ƒŽ –‘ –Š‡ ƒ” ‘ˆ ”ƒ†‹—• ȋ”ȌǤ

• „‘–Š –Š‡ •Ž‘’‡ ƒ† ‹–• ”ƒ–‡ ‘ˆ Šƒ‰‡ ˜ƒ”› ˆ‘” ƒ —”˜‡ǡ Ž‡– —• ϐ‹† –Š‡ ‰‡‡”ƒŽ ‡š’”‡••‹‘ ˆ‘”
—”˜ƒ–—”‡ ‘” ”ƒ†‹—• ‹ –‡”• ‘ˆ ȋ†›Ȁ†šȌ ƒ† ȋ† ›Ȁ†š Ȍ
ʹ
ʹ
‘•‹†‡” ƒ —”˜‡ ‹ –Š‡ Ǯš-›ǯ ’Žƒ‡ ƒ• •Š‘™ ‹ ȏ ‹‰ ͳǤͳͳȐǤ ”ƒ™ –ƒ‰‡–• ƒ– –™‘ ’‘‹–• •‡’ƒ”ƒ–‡†
„› ƒ ‡Ž‡‡–ƒŽ ƒ” Ž‡‰–Š ȋ†•ȌǤ Š‡ ƒ”
Ž‡‰–Š •—„–‡†• ƒ ƒ‰Ž‡ ȋ†ɅȌ ƒ– –Š‡
‡–‡”Ǥ Š‹• ‹• ‡šƒ –Ž› –Š‡ ƒ‰Ž‡ „‡–™‡‡
–Š‡ –ƒ‰‡–• ƒ– ’‘‹– ȋͳȌ ƒ† ȋʹȌǤ

[Fig 1.11: radius of curvature]

dy 2

2
2
Therefore, we have: Rdθ = dx + dy or Rdθ = dx 1 +
dx

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 12