Page 37 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Document Title
Fundamentals of Stress and Vibration 2. Engineering Mechanics Chapter
[A Practical guide for aspiring Designers / Analysts]

ʹǤ͸ ‡™–‘ǯ• ƒ™• ‘ˆ ‘–‹‘

ƒ› ‘ˆ –Š‡ „ƒ•‹ ‡‰‹‡‡”‹‰ ’”‘„Ž‡• ƒ „‡ •‘Ž˜‡† —•‹‰ –Š‡ ‡™–‘ǯ• Žƒ™• ‘ˆ ‘–‹‘Ǥ Š‡
‘•– ‘‘ ƒ’’Ž‹ ƒ–‹‘• ƒ”‡ǣ
· ‡Š‹ Ž‡ †›ƒ‹ •
· ‡ Šƒ‹••
Š‡ –Š”‡‡ Žƒ™• ‘ˆ ‘–‹‘ –Šƒ– ‰‘˜‡” Žƒ••‹ ƒŽ ‡ Šƒ‹ •ǡ ‹˜‘Ž˜‡ ƒ ‹’‘”–ƒ– ‘ ‡’– ƒŽŽ‡†
‹‡”–‹ƒǤ
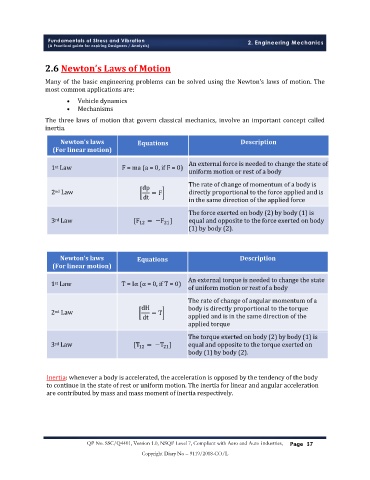
Newton’s laws Equations Description
(For linear motion)

An external force is needed to change the state of
1 Law F = ma (a = 0, if F = 0)
st
uniform motion or rest of a body
The rate of change of momentum of a body is
dp
2 Law = F directly proportional to the force applied and is
nd
dt in the same direction of the applied force
The force exerted on body (2) by body (1) is
3 Law [F 12 = −F ] equal and opposite to the force exerted on body
rd
21
(1) by body (2).

Newton’s laws Equations Description
(For linear motion)

An external torque is needed to change the state
1 Law T = Iα (α = 0, if T = 0)
st
of uniform motion or rest of a body
The rate of change of angular momentum of a
dH body is directly proportional to the torque
2 Law = T
nd
dt applied and is in the same direction of the
applied torque
The torque exerted on body (2) by body (1) is
3 Law [T 12 = −T ] equal and opposite to the torque exerted on
rd
21
body (1) by body (2).

Inertia: whenever a body is accelerated, the acceleration is opposed by the tendency of the body
to continue in the state of rest or uniform motion. The inertia for linear and angular acceleration
are contributed by mass and mass moment of inertia respectively.

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries, Page 37 age 37
P
Copyright Diary No – 9119/2018-CO/L