Page 42 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp
P. 42
Document Title
Fundamentals of Stress and Vibration Chapter Title
[A Practical guide for aspiring Designers / Analysts] 2. Engineering Mechanics
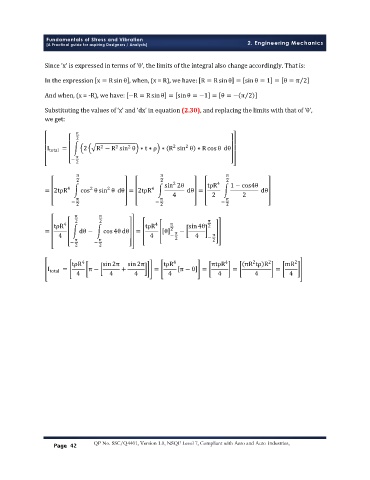
Since ‘x’ is expressed in terms of ‘θ’, the limits of the integral also change accordingly. That is:
In the expression x = R sin θ , when, (x = R), we have: R = R sin θ = sinθ = 1 = θ = π 2
And when, (x = -R), we have: −R = R sinθ = sin θ = −1 = θ = − π 2
Substituting the values of ‘x’ and ‘dx’ in equation (2.30), and replacing the limits with that of ‘θ’,
we get:
π
2
2 2 2 2 2
I
total = 2 R − R sin θ ∗ t ∗ ρ ∗ R sin θ ∗ R cos θ dθ
− π
2
π π π
2 2 sin 2θ tρR 4 2 1 − cos4θ
2
2
4
2
4
= 2tρR cos θ sin θ dθ = 2tρR dθ = dθ
π π 4 2 π 2
− 2 − 2 − 2
π π
2 2 π
tρR 4 tρR 4 π sin4θ 2
= dθ − cos 4θ dθ = θ 2 π − π
4 − π − π 4 − 2 4 − 2
2 2
2
tρR 4 sin 2π sin2π tρR 4 πtρR 4 πR tρ R 2 mR 2
I = π − + = π − 0 = = =
total
4 4 4 4 4 4 4
Page 42 QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,